Question

How many planes can be made to pass through three distinct non-collinear points?
(a) 3
(b) 2
(c) 1
(d) 0

Answer 1

Hint: First, before proceeding for this, we must know the following condition to make a plane that at least one point should pass from the plane to get that plane in existence. Then, we have three distinct non-collinear points: let A, B and C be those points that are non-collinear in nature means that are not in a straight line and have different places of marking. Then, by considering different cases for the planes to exist, we will get the condition for the maximum number of planes from three non collinear points as an answer.

Complete step-by-step answer:
In this question, we are supposed to find the number of planes that can be made to pass through three distinct non-collinear points.
So, before proceeding for this, we must know the following condition to make a plane that at least one point should pass from the plane to get that plane in existence.
Now, we have three distinct non-collinear points. Let A, B and C be those points that are non-collinear in nature means that are not in a straight line and have different places of marking.
So, we can draw the non-collinear points A, B and C as:

Now, it is clear from the figure that the three points are not in the straight line which makes them non-collinear.
Then, we need to get the maximum number of planes that can pass through these points.
So, we can pass a place through AB and C alone which makes the count as 2 planes.
Similarly, taking two points at a time for a plane and a single point for another plane makes the count of planes at maximum is 2.
Now, if we take all three points in one plane which makes the count of planes as 1.
Then, we can take three planes from all three points A,B and c which are different which makes the count of planes 3 as:

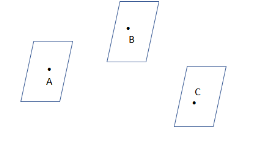
So, the maximum number of planes that can be made to pass through three distinct non-collinear points is 3.
So, the correct answer is “Option A”.

Note: Now, the only mistake in this type of question we occur is that we give the answer as 1 and mark option (c) as correct which is a wrong choice because most of the time the conditions mentioned in the question are collinear to confuse the candidate. But, in this question the points are non-collinear, so three planes can exist at maximum.