Question

Places A and B are 100km apart on a highway. One car starts from A and another from B at the same time. If the cars travel in the same direction at different speeds , they meet in 5 hrs. If they travel towards each other they meet in one hr. What is the difference of speeds in km/hr of the two cars ?

Answer 1

Hint: If the cars are moving in same direction use the formula
\[\left( {SA - SB} \right) = \dfrac{{dis\tan ce\,\,between\,them}}{{time\,taken\,by\,them\,to\,meet}}\]
If the cars are moving in opposite direction use the formula
\[\left( {SA + SB} \right) = \dfrac{{dis\tan ce\,\,between\,them}}{{time\,taken\,by\,them\,to\,meet}}\]
Solve these two equations to get the SA and SB

Complete step-by-step answer:
The objective of the problem is to find the difference of speeds of the two cars.
 Given that the two cars A and B are \[100km\]apart on a highway. It is also given that they start from A and another from B at the same time respectively.
Also , they travel in the same direction at different speeds they meet in 5hrs. If they travel towards each other they meet in one hr.
Let us consider the speed of car A as SA and the speed of the car B as SB
We have to solve this problem in two cases

Case 1: When cars are moving in same direction

Let two cars meet at a point C

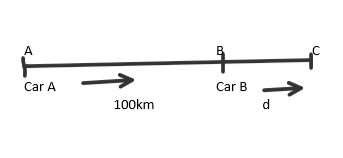
Distance from B and C is d
It is given both cars meet after 5hrs
We get, time taken by car A to reach C= time taken by car B to reach C=5hrs
We know that \[time = \dfrac{{dis\tan ce}}{{speed}}\]
Therefore , time taken by car A to reach C\[ = \dfrac{{100 + d}}{{SA}} = 5 \to \left( 1 \right)\]
Time taken by the car B to reach C \[ = \dfrac{d}{{SB}} = 5 \to \left( 2 \right)\]
From equation (2), we get \[d = 5SB\]
Substitute the value of d in equation (1) , we get

\[\
  \dfrac{{100 + 5SB}}{{SA}} = 5 \\
\Rightarrow 100 + 5SB = 5SA \\
\ \]
\[\
  5SA - 5SB = 100 \\
\Rightarrow SA - SB = 20 \to \left( 3 \right) \\
\ \]
Case (2): When cars moving in opposite direction

Let us consider cars meet at point C

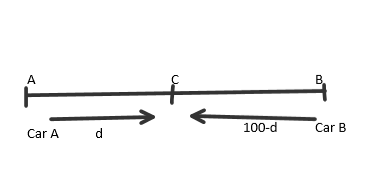
Let AC=d
\[\
  AC + CB = 100 \\
\Rightarrow CB = 100 - d \\
\ \]
 It is given that the cars meet after one hour
We get time taken by car A to reach C= time taken by car B to reach C=1hr
We know that \[time = \dfrac{{dis\tan ce}}{{speed}}\]
Therefore , time taken by car A to reach C\[ = \dfrac{d}{{SA}} = 1 \to \left( 4 \right)\]
Time taken by the car B to reach C \[ = \dfrac{{100 - d}}{{SB}} = 1 \to \left( 5 \right)\]
From equation(4) \[d = SA\]
Substitute above equation in (5)
\[\
  \dfrac{{100 - SA}}{{SB}} = 1 \\
\Rightarrow 100 - SA = SB \\
\Rightarrow SA + SB = 100 \to \left( 6 \right) \\
\ \]
On solving equations (3) and (6), we get
\[\
  SA - SB + SA + SB = 20 + 100 \\
\Rightarrow 2SA = 120 \\
\Rightarrow SA = 60 \\
\ \]
Therefore speed of car A is \[60km/hr\]
For the speed of B substitute SA in equation 6 we get,
\[\
  60 + SB = 100 \\
\Rightarrow SB = 40 \\
\ \]
Therefore speed of car B is \[40km/hr\].

Note: We can check the answers by putting the values of SA and SB in equations and check if they satisfy the equation or not.