Question

Places A and B are 100km apart on a highway. One car starts at A and another from B at the same time. If the cars travel in the same direction at different speeds, they meet in 5 hours. If they travel towards each other, they meet in 1 hour. What are the speeds of two cars?

Answer 1

Hint: We solve this problem by assuming the meeting points in two different conditions as C and D then the rough figure of given information will be

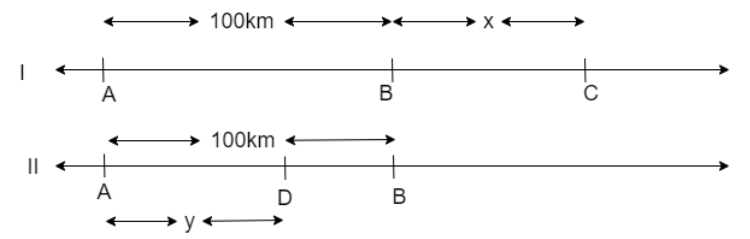
We assume the speeds of two cars as some variables then we use the formula of time as
\[Time=\dfrac{\text{Distance}}{\text{speed}}\]
We use the two conditions given in the question to find the speeds of two cars.

Complete step by step answer:
We are given that the distance between two points A and B as 100km.
Let us assume that the speed of car that started at A as \['{{V}_{a}}'\]
Let us assume that the speed of car that started at B as \['{{V}_{b}}'\]
Now, let us consider the first case that is they travel in same direction.
(i) Travel in same direction.
From the figure we can see that the two cars meet at point C which is \['x'\] distance from B.
So, we can say that first car covered a total distance of \['100+x'\] and second car covered a distance of \['x'\] to meet at point C.
Let us assume that the time taken by first car to reach point C as \['{{t}_{1}}'\]
We know that the formula for time as
\[Time=\dfrac{\text{Distance}}{\text{speed}}\]
By using this formula we get
\[\Rightarrow {{t}_{1}}=\dfrac{100+x}{{{V}_{a}}}\]
Similarly, by assuming the time taken by second car to reach point C as \['{{t}_{2}}'\] we get
\[\Rightarrow {{t}_{2}}=\dfrac{x}{{{V}_{b}}}\]
We are given that the two cars meet in 5 hours when moved in same direction which means that both cars took 5 hours to meet at point C

So, we can write from the above condition that is
\[\begin{align}
  & \Rightarrow {{t}_{1}}={{t}_{2}}=5 \\
 & \Rightarrow \dfrac{100+x}{{{V}_{a}}}=\dfrac{x}{{{V}_{b}}}=5 \\
\end{align}\]
Now, by separating the terms of unknown variables to constant we get
\[\begin{align}
  & \Rightarrow \dfrac{100+x}{{{V}_{a}}}=5 \\
 & \Rightarrow 100+x=5{{V}_{a}} \\
 & \Rightarrow x=5{{V}_{a}}-100 \\
\end{align}\]
Now, by taking the other terms we get
\[\begin{align}
  & \Rightarrow \dfrac{x}{{{V}_{b}}}=5 \\
 & \Rightarrow x=5{{V}_{b}} \\
\end{align}\]
By substituting the value of \['x'\] in above equation we get
\[\begin{align}
  & \Rightarrow 5{{V}_{a}}-100=5{{V}_{b}} \\
 & \Rightarrow {{V}_{a}}-{{V}_{b}}=20........equation(i) \\
\end{align}\]
Now let us go for the second condition that is the cars move in opposite direction
(ii) Travel in opposite direction.
From the figure we can see that the two cars meet at point D which is \['y'\] distance from A.
So, we can say that first car covered a total distance of \['y'\] and second car covered a distance of \['100-y'\] to meet at point D.
Let us assume that the time taken by first car to reach point D as \['{{t}_{3}}'\]
We know that the formula for time as
\[Time=\dfrac{\text{Distance}}{\text{speed}}\]
By using this formula we get
\[\Rightarrow {{t}_{3}}=\dfrac{y}{{{V}_{a}}}\]

Similarly, by assuming the time taken by second car to reach point C as \['{{t}_{4}}'\] we get
\[\Rightarrow {{t}_{4}}=\dfrac{100-y}{{{V}_{b}}}\]
We are given that the two cars meet in 1 hour when moved in same direction which means that both cars took 1 hour to meet at point D
So, we can write from the above condition that is
\[\begin{align}
  & \Rightarrow {{t}_{3}}={{t}_{4}}=1 \\
 & \Rightarrow \dfrac{y}{{{V}_{a}}}=\dfrac{100-y}{{{V}_{b}}}=1 \\
\end{align}\]
Now, by separating the terms of unknown variables to constant we get
\[\Rightarrow y={{V}_{a}}\]
Now, by taking the other terms we get
\[\Rightarrow \dfrac{100-y}{{{V}_{b}}}=1\]
By substituting the value of \['y'\] in above equation we get
\[\begin{align}
  & \Rightarrow 100-{{V}_{a}}={{V}_{b}} \\
 & \Rightarrow {{V}_{a}}+{{V}_{b}}=100........equation(ii) \\
\end{align}\]
Now, by adding the equation (i) and equation (ii) we get
\[\begin{align}
  & \Rightarrow \left( {{V}_{a}}-{{V}_{b}} \right)+\left( {{V}_{a}}+{{V}_{b}} \right)=20+100 \\
 & \Rightarrow {{V}_{a}}=\dfrac{120}{2}=60kmph \\
\end{align}\]
By substituting the above value in equation (i) we get
\[\begin{align}
  & \Rightarrow 60-{{V}_{b}}=20 \\
 & \Rightarrow {{V}_{b}}=40kmph \\
\end{align}\]

Therefore the speeds of two cars are 60kmph and 40kmph.

Note: We have a shortcut for two conditions that is relative velocity.
Let us assume that the speed of car that started at A as \['{{V}_{a}}'\]
Let us assume that the speed of car that started at B as \['{{V}_{b}}'\]
If \['{{t}_{1}}'\] is the time taken by two cars to meet when they move in same direction then by using the relative velocity we get
\[\Rightarrow {{t}_{1}}=\dfrac{d}{{{V}_{a}}-{{V}_{b}}}\]
Here, \['d'\] is the distance between two cars that is 100km.
By using this formula we get
\[\begin{align}
  & \Rightarrow 5=\dfrac{100}{{{V}_{a}}-{{V}_{b}}} \\
 & \Rightarrow {{V}_{a}}-{{V}_{b}}=20.......equation(i) \\
\end{align}\]
Similarly, if \['{{t}_{2}}'\] is the time taken by two cars to meet when they travel in opposite direction hen the relative velocity is given as
\[\Rightarrow {{t}_{2}}=\dfrac{d}{{{V}_{a}}+{{V}_{b}}}\]
Here, \['d'\] is the distance between two cars that is 100km.
By using the above formula we get
\[\begin{align}
  & \Rightarrow 1=\dfrac{100}{{{V}_{a}}+{{V}_{b}}} \\
 & \Rightarrow {{V}_{a}}+{{V}_{b}}=100......equation(ii) \\
\end{align}\]
Now, by adding the equation (i) and equation (ii) we get
\[\begin{align}
  & \Rightarrow \left( {{V}_{a}}-{{V}_{b}} \right)+\left( {{V}_{a}}+{{V}_{b}} \right)=20+100 \\
 & \Rightarrow {{V}_{a}}=\dfrac{120}{2}=60kmph \\
\end{align}\]
By substituting the above value in equation (i) we get
\[\begin{align}
  & \Rightarrow 60-{{V}_{b}}=20 \\
 & \Rightarrow {{V}_{b}}=40kmph \\
\end{align}\]
Therefore the speeds of two cars are 60kmph and 40kmph.