Question

What is the period of $\cos\left(\dfrac{x}{3}\right)$?

Answer 1

Hint: Fundamental period or period of a function is defined as the interval at which the function repeats its value. Here, we are provided with a function whose period we have to find out. Mathematically, the period is valued $K \in \mathbb{R}-\{0\} s.t. f\left(x+k\right)=f\left(x\right)$.
$cos\left(x\right)$ has period $2 \pi$.

Complete step-by-step solution:
We are given the function $\cos\left(\dfrac{x}{3}\right)$. And as we know that the $\cos\left(x\right)$ is a periodic function with the period $2\pi$. So, our function is also periodic with some fundamental period. Since when there is $x$ in $\cos$ function it repeats its value after $2\pi$ . That is here the function will repeat its value after $6\pi$.
Other periods can be given as:
$F=\{ 6n \pi : n \in \textbf{Z} \}$
But the fundamental period is basically the minimum of the set from the positive side.
Mathematically, if the period of $f\left(x\right)$ is 'p' then the period of $f\left(ax\right)$ will be $\dfrac{p}{a}$.
Using this fact, we know the period of $cos\left(x\right)$ is $2\pi$ then, period of $\cos\left(\dfrac{x}{3}\right)$ will be $3\times\left(2\pi\right)$ $\implies$ $6\pi$. What we have done is, we have to divide the coefficient of 'x' by the fundamental period of the function.
The graph for $\cos\left(\dfrac{x}{3}\right)$ is as below:

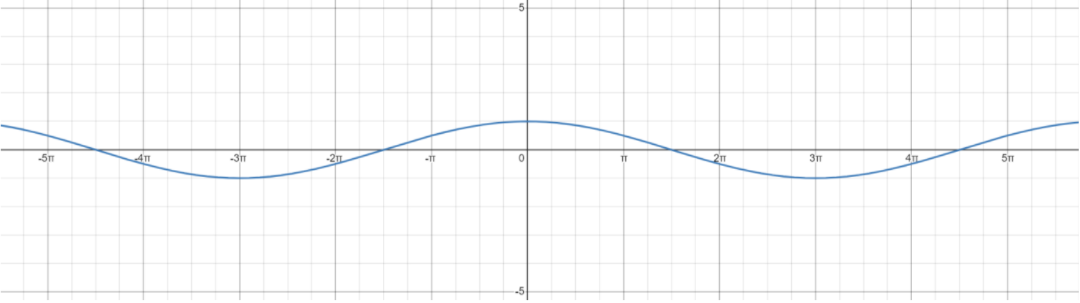
So, the fundamental period has been found.

Note: Since, there is a coefficient of $\dfrac{1}{3}$ with the variable 'x' inside cos, it is a general mistake to divide the standard period by 3 and write the result i.e. you can NOT write the period to be $\dfrac{2\times\pi}{3}$. This would be an incorrect solution. Moreover, do not write any multiple above the least one, because then that would not be the principle period.