Question

What is the perimeter of the triangle with the corners at \[(7,\ 5)\] , \[(1,\ 2)\] and \[(4,\ 7)\] ?

Answer 1

Hint: In this question, we need to find the perimeter of the triangle. A triangle is a geometric figure which has three sides, three angles and three vertices . The sum of all internal angles of the triangle is always equal to \[180^{\circ}\]. This is known as the property of the triangle. The perimeter of the triangle is nothing but it is the total length of the boundary of the triangle. In the case of a triangle, we can find it by adding the lengths of its three sides. The three corners of the triangle are given by using the distance formula, we can find the sides of the triangle. Then we can find the perimeter of the triangle.

Formula used:
\[\text{Perimeter} = A + B + C\]
Where \[A, B\] and \[C\] are the sides of the triangle.
The formula for the distance between two points \[(a,\ b)\] and \[(c,\ d)\] is
\[D = \sqrt{\left( c – a \right)^{2} + \left( d – b \right)^{2}}\]

Complete step-by-step solution:
Given, corners at \[(7,5)\] , \[(1,2)\] and \[(4,7)\]

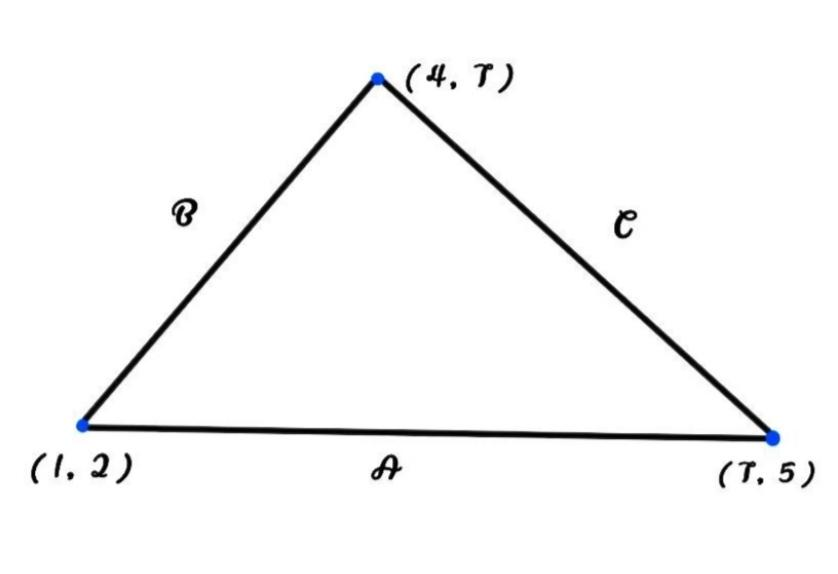
Let us assume the given points as \[x,\ y\] and \[z\] . That is \[x = (7,\ 5)\] , \[y = (1,\ 2)\] and \[z = (4,\ 7)\] .
First we can find the distance between two points.
Distance between \[x\] and \[y\],
\[A = \sqrt{\left( 1 – 7 \right)^{2} + \left( 2 – 5 \right)^{2}}\]
On simplifying,
We get,
\[A = \sqrt{\left( - 6 \right)^{2} + \left( - 3 \right)^{2}}\]
\[\Rightarrow \ A = \sqrt{36 + 9}\]
On further simplifying,
We get
\[A = \sqrt{45}\]
Distance between \[y\] and \[z\],
\[B = \sqrt{\left( 4 – 1 \right)^{2} + \left( 7 – 2 \right)^{2}}\]
On simplifying,
We get,
\[B = \sqrt{\left( 3 \right)^{2} + \left( 5 \right)^{2}}\]
\[\Rightarrow \ B = \sqrt{9 + 25}\]
On further simplifying,
We get,
\[B = \sqrt{34}\]
Distance between \[z\] and \[x\],
\[C = \sqrt{\left( 4 – 7 \right)^{2} + \left( 7 – 5 \right)^{2}}\]
On simplifying,
We get,
\[C = \sqrt{\left( - 3 \right)^{2} + \left( 2 \right)^{2}}\]
\[\Rightarrow \ C = \sqrt{9 + 4}\]
On further simplifying,
We get,
\[C = \sqrt{13}\]
Now \[\text{Perimeter} = A + B + C\]
\[\text{Perimeter} = \sqrt{45} + \sqrt{34} + \sqrt{13}\]
We need to find the value of square roots.
\[\text{Perimeter} = 6.7 + 5.8 + .36\]
On adding,
We get,
\[\text{Perimeter} = 16.1\ units\] .
Thus we get the perimeter of the triangle is \[16.1\ units\]
Final answer :
The perimeter of the triangle is \[16.1\ units\].

Note: The concept used in this problem to find the perimeter of the triangle is distance between two points. Square root of a number is nothing but a value in which it turns to the original number when it is multiplied by itself. Suppose \[c\] is a square root of \[b\] then it is represented as \[c\ = \ \sqrt{b}\] . For example, \[4\] is the square root of \[16\] then it is represented as \[4 = \sqrt{16}\] . Mathematically, the symbol \[\sqrt{}\ \]
 is known as the radical sign which is used to represent the square root. It is basically one of the methods to solve the quadratic equation . In order to find the square root, we can use two methods
1.Long division method
2.Factorisation method
It’s easy to memorize the square root values of the numbers \[1\] to \[15\] . After that number we need to use any of the methods to find the square root values.