Question

What is the perimeter of a regular octagon with a radius of length 20?

Answer 1

Hint: Here in this question, we have to find the perimeter of a regular octagon of given radius of length \[r = 20\] . First, we have to find the length \[l\] of each side of octagon using a distance formula \[l = \sqrt {{{\left( {{y_2} - {y_1}} \right)}^2} + {{\left( {{x_2} - {x_1}} \right)}^2}} \] and later find a perimeter using a formula \[P = 8 \times l\,\] . If we are finding the perimeter of a regular octagon, then we know that all eight sides are equal lengths, so we can simplify the formula using multiplication operation to get the required solution.

Complete step-by-step answer:
In geometry, perimeter can be defined as the path or the boundary that surrounds a shape. It can also be defined as the length of the outline of a shape.
If a octagon is regular, then all the sides are equal in length, and eight angles are of equal measures
Consider a regular octagon having radius of length \[r = 20\] , which is same for vertices of pentagons.
In figure, the red circle circumscribes the outer radius and the green circle the inner one.

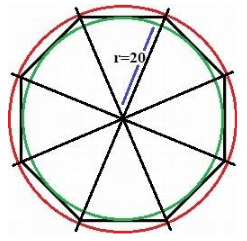
Let consider \[r = 20\] be the outer radius - that is the radius of the red circle.
Then, the vertices of the octagon centred at origin i.e., \[\left( {0,0} \right)\] are at \[\left( { \pm \,r,0} \right)\] , \[\left( {0, \pm \,r} \right)\] and \[\left( { \pm \,\dfrac{r}{{\sqrt 2 }}, \pm \,\dfrac{r}{{\sqrt 2 }}} \right)\] .
So the length of one side of regular octagon is distance between \[\left( {r,\,0} \right)\] and \[\left( {\dfrac{r}{{\sqrt 2 }},\,\dfrac{r}{{\sqrt 2 }}} \right)\]
Let consider a distance formula \[l = \sqrt {{{\left( {{y_2} - {y_1}} \right)}^2} + {{\left( {{x_2} - {x_1}} \right)}^2}} \] , on substituting we have
 \[ \Rightarrow \,\,l = \sqrt {{{\left( {\dfrac{r}{{\sqrt 2 }} - 0} \right)}^2} + {{\left( {\dfrac{r}{{\sqrt 2 }} - r} \right)}^2}} \]
 \[ \Rightarrow \,\,l = \sqrt {{{\left( {\dfrac{r}{{\sqrt 2 }}} \right)}^2} + {{\left( {\dfrac{r}{{\sqrt 2 }} - r} \right)}^2}} \]
 \[ \Rightarrow \,\,l = \sqrt {{r^2}{{\left( {\dfrac{1}{{\sqrt 2 }}} \right)}^2} + {r^2}{{\left( {\dfrac{1}{{\sqrt 2 }} - 1} \right)}^2}} \]
Take \[{r^2}\] to outside, then
 \[ \Rightarrow \,\,l = r\sqrt {{{\left( {\dfrac{1}{{\sqrt 2 }}} \right)}^2} + {{\left( {\dfrac{1}{{\sqrt 2 }} - 1} \right)}^2}} \]
Simplify using a algebraic identity \[{\left( {a - b} \right)^2} = {a^2} + {b^2} - 2ab\] , we have
 \[ \Rightarrow \,\,l = r\sqrt {\dfrac{1}{{{{\left( {\sqrt 2 } \right)}^2}}} + \dfrac{1}{{{{\left( {\sqrt 2 } \right)}^2}}} + 1 - \dfrac{2}{{\sqrt 2 }}} \]
On simplification, we get
 \[ \Rightarrow \,\,l = r\sqrt {\dfrac{1}{2} + \dfrac{1}{2} + 1 - \dfrac{2}{{\sqrt 2 }}} \]
 \[ \Rightarrow \,\,l = r\sqrt {1 + 1 - \dfrac{2}{{\sqrt 2 }}} \]
 \[ \Rightarrow \,\,l = r\sqrt {2 - \sqrt 2 } \] ------(1)
Which is the length of the each side of the regular octagon when \[r\] be the outer radius.
Then perimeter of regular octagon is
 \[ \Rightarrow \,\,P = 8 \times l\,\]
On substituting equation (1), we have
 \[ \Rightarrow \,\,P = 8 \times r\sqrt {2 - \sqrt 2 } \]
given \[r = 20\] , then
 \[ \Rightarrow \,\,P = 8 \times 20\sqrt {2 - \sqrt 2 } \]
 \[ \Rightarrow \,\,P = 160\sqrt {2 - \sqrt 2 } \]
On using calculator, we get the exact value
 \[ \Rightarrow \,\,P = 160\sqrt {2 - \sqrt 2 } \simeq 122.46\]
Now, consider \[{r_1} = 20\] be the inner radius - that is the radius of the green circle
The inner radius will be \[{r_1} = r\cos \theta \]
From the figure we have \[\theta = \dfrac{\pi }{8}\] , then
 \[ \Rightarrow \,\,{r_1} = r\cos \left( {\dfrac{\pi }{8}} \right)\]
By using a calculator, the value of \[\cos \left( {\dfrac{\pi }{8}} \right) = \dfrac{{\sqrt {2 + \sqrt 2 } }}{2}\] , then
 \[ \Rightarrow \,\,{r_1} = r\left( {\dfrac{{\sqrt {2 + \sqrt 2 } }}{2}} \right)\]
On cross multiplication, we have
 \[ \Rightarrow \,r = \,\dfrac{{2{r_1}}}{{\sqrt {2 + \sqrt 2 } }}\] ------(2)
On substituting equation (2) in (1), we get the length of each side i.e.,
 \[ \Rightarrow \,\,l = \dfrac{{2{r_1}}}{{\sqrt {2 + \sqrt 2 } }}\sqrt {2 - \sqrt 2 } \]
 \[ \Rightarrow \,\,l = 2{r_1}\dfrac{{\sqrt {2 - \sqrt 2 } }}{{\sqrt {2 + \sqrt 2 } }}\]
To rationalize the denominator, we have to multiply and divide the RHS by \[\sqrt {2 + \sqrt 2 } \] , then
 \[ \Rightarrow \,\,l = 2{r_1}\dfrac{{\sqrt {2 - \sqrt 2 } }}{{\sqrt {2 + \sqrt 2 } }} \times \dfrac{{\sqrt {2 + \sqrt 2 } }}{{\sqrt {2 + \sqrt 2 } }}\]
 \[ \Rightarrow \,\,l = 2{r_1}\dfrac{{\left( {\sqrt {2 - \sqrt 2 } } \right)\left( {\sqrt {2 + \sqrt 2 } } \right)}}{{\left( {\sqrt {2 + \sqrt 2 } } \right)\left( {\sqrt {2 + \sqrt 2 } } \right)}}\]
 \[ \Rightarrow \,\,l = 2{r_1}\dfrac{{\sqrt {\left( {2 - \sqrt 2 } \right)\left( {2 + \sqrt 2 } \right)} }}{{{{\left( {\sqrt {2 + \sqrt 2 } } \right)}^2}}}\]
On simplification, we get
 \[ \Rightarrow \,\,l = 2{r_1}\dfrac{{\sqrt {4 + 2\sqrt 2 - 2\sqrt 2 - 2} }}{{2 + \sqrt 2 }}\]
 \[ \Rightarrow \,\,l = 2{r_1}\dfrac{{\sqrt 2 }}{{2 + \sqrt 2 }}\] -----------(3)
Which is the length of each side of the regular octagon when \[r\] be the inner radius.
Then perimeter of regular octagon is
 \[ \Rightarrow \,\,P = 8 \times l\,\]
On substituting equation (1), we have
 \[ \Rightarrow \,\,P = 8 \times 2{r_1}\dfrac{{\sqrt 2 }}{{2 + \sqrt 2 }}\]
 \[ \Rightarrow \,\,P = 16{r_1}\dfrac{{\sqrt 2 }}{{2 + \sqrt 2 }}\]
given \[{r_1} = 20\] , then
 \[ \Rightarrow \,\,P = 16\left( {20} \right)\dfrac{{\sqrt 2 }}{{2 + \sqrt 2 }}\]
 \[ \Rightarrow \,\,P = 320\dfrac{{\sqrt 2 }}{{2 + \sqrt 2 }}\]
On using calculator, we get the exact value
 \[ \Rightarrow \,\,P = 320\dfrac{{\sqrt 2 }}{{2 + \sqrt 2 }} \simeq 132.55\]
Hence, the perimeter of regular octagon of radius 20 is
If the outer radius is 20, then the perimeter is: \[P = 160\sqrt {2 - \sqrt 2 } \simeq 122.46\]
If the inner radius is 20, then the perimeter is: \[\,P = 320\dfrac{{\sqrt 2 }}{{2 + \sqrt 2 }} \simeq 132.55\]
So, the correct answer is “$\simeq 132.55$”.

Note: While determining the perimeter we use the formula. The unit for the perimeter will be the same as the unit of the length of a side or polygon. Whereas the unit for the area will be the square of the unit of the length of a polygon. We should not forget to write the unit with a final answer and we should also know about regular and irregular polygons.