Question

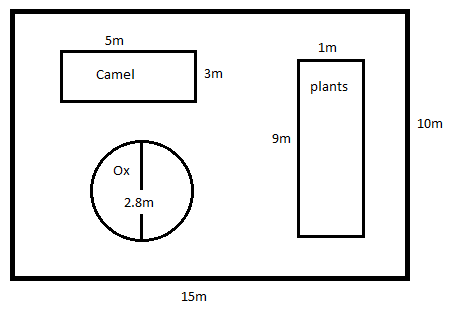
People of Khejarli village take good care of plants, trees and animals. They say that plants and animals can survive without us, but we cannot survive without them. Inspired by elders, Amrita marked some land for her pets (camel and ox) and plants. Find the ratio of the areas kept for animals and plants to the living area.

Answer 1

Hint:
We can find the area of the land for camels by finding the area of the rectangle. Then we can find the area of the land for plants by taking the area of the rectangle labelled plants. We can also find the area for ox by finding the area of the circle. We can add these areas to get the total area for plants and animals. We can find the total area of the land by finding the area of the larger rectangle. Then we can subtract the area for the plants and animals from the total area of the land. Then we can take the required ratio by dividing and simplifying.

Complete step by step solution:
From the figure, the total area of the land is given by area of the rectangle with sides 15m and 10m
Total area of the land, $A = l \times b$
On substituting values we get,
 $ \Rightarrow A = 15 \times 10$
On simplification we get,
 $ \Rightarrow A = 150{m^2}$
Now we can find the area for the camels.
 $ \Rightarrow {A_{camel}} = l \times b$
On substituting the values we get,
 $ \Rightarrow {A_{camel}} = 5 \times 3$
On simplification we get,
 $ \Rightarrow {A_{camel}} = 15{m^2}$
Now the area for the plants is given by,
 $ \Rightarrow {A_{plants}} = l \times b$
On substituting the values we get,
 $ \Rightarrow {A_{plants}} = 9 \times 1$
 On simplification we get,
 $ \Rightarrow {A_{camel}} = 9{m^2}$
Now we can find the area for ox.
From the figure, the radius of the circle is \[r = \dfrac{{2.8}}{2} = 1.4m\]
Then its area is given by, ${A_{ox}} = \pi {r^2}$
On substituting the values we get,
 $ \Rightarrow {A_{ox}} = \dfrac{{22}}{7}{\left( {1.4} \right)^2}$
On simplification we get,
 $ \Rightarrow {A_{ox}} = 22 \times 0.2 \times 1.4$
On multiplying we get,
 $ \Rightarrow {A_{ox}} = 6.16{m^2}$
Now we can find the total area for the plants, ox and camels by taking the sum of their areas.
 $ \Rightarrow {A_{total}} = {A_{ox}} + {A_{camel}} + {A_{plants}}$
On substituting the values we get,
 $ \Rightarrow {A_{total}} = 15 + 9 + 6.16$
On adding all the values we get,
 $ \Rightarrow {A_{total}} = 30.16$
Now we have the area for animals and plants. We can find the area for living by subtracting it from the total area.
Therefore, the area of living is given by.
 $ \Rightarrow {A_{living}} = A - {A_{total}}$
On substituting the values we get,
 $ \Rightarrow {A_{living}} = 150 - 30.16$
On subtracting we get,
 $ \Rightarrow {A_{living}} = 119.84{m^2}$
Now we can take the ratio of area for plants and animals to the living area.
 $ \Rightarrow ratio = \dfrac{{{A_{total}}}}{{{A_{living}}}}$
On substituting the values, we get,
 $ \Rightarrow ratio = \dfrac{{30.16}}{{119.84}}$
On simplification, we get,
 $ \Rightarrow ratio = \dfrac{{7.54}}{{29.96}}$
On multiplying the numerator and denominator by 50, we get,
 $ \Rightarrow ratio = \dfrac{{377}}{{1498}}$

Therefore, the required ratio is $377:1498$

Note:
The concept of area of rectangles and circles is used to solve this problem. While calculating the area of the circular part, we must take care that the diameter is given, not the radius. So, we need to find the radius to find the area. While taking the ratios, order is important. So, we must read the question carefully before taking the ratio. Here the living area means the area that can be used for our living or the area which is not occupied by pets or plants.