Question

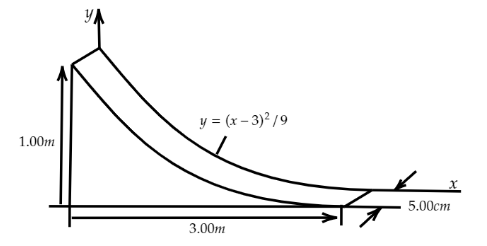
Pat builds a track for his model car out of solid wood as shown in figure. The track is $5.00\,cm$ wide, $1.00\,m$ high, and $3.00\,m$ long. The runway is cut so that it forms a parabola with the equation \[y = \dfrac{{{{(x - 3)}^2}}}{9}\]. Locate the horizontal coordinates of the center of gravity of this track.

Answer 1

Hint: For geometrical objects the centre of gravity lies at the focus or centre of the object. Use this property to find the horizontal coordinates of the center of gravity of this track. Use the equation of parabola to find the center of gravity of this track.

Complete step by step answer:
Here, Pat builds a track for his model car out of solid wood and the track is 5.00 cm wide, 1.00 m high, and 3.00 m long. The runway is cut so that it forms a parabola with the equation \[y = \dfrac{{{{(x - 3)}^2}}}{9}\]. We know that, the equation of parabola with axis along the $y$ axis is given by,
\[{(x - \alpha )^2} = 4a(y - \beta )\]
where, \[\left( {\alpha ,a + \beta } \right)\] is the focus of the parabola.
So, rewriting the equation of the ramp we have,
\[{(x - 3)^2} = 4(\dfrac{9}{4})y\]
So, from the equation we can see that,
\[\alpha = 3\], \[\beta = 0\], \[a = \dfrac{9}{4}\]
So, the focus of the parabola is at, \[(3,\dfrac{9}{4})\]. Hence, the horizontal component of the centre of gravity will be the $x$ component of the focus of the parabola.

Hence, the horizontal component of the centre of gravity is \[3\].

Note: We can also easily say that the $y$ component of the focus is the vertical coordinate of centre of gravity and the $Z$ component will lie at the half length of the depth of the track. To find the centre of gravity of geometrical objects we can use symmetry also for symmetrical objects. For symmetrical objects the centre of gravity lies on the centre of the objects.