Question

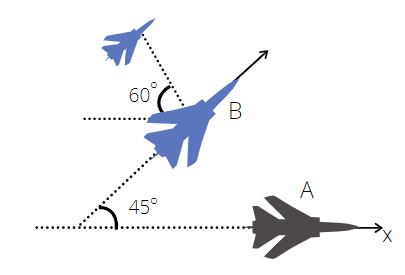
Passengers in the jet transport A flying east at a speed of \[800km/h\] observe a second jet plane B that passes under the transport in horizontal flight. Although the nose of B is pointed in the \[45{}^\circ \] north east direction, plane B appears to the passengers in A to be moving away from the transport at the \[60{}^\circ \] angle as shown. The true velocity of B is :

\[\begin{align}
  & A)586km/h \\
 & B)400\sqrt{2}km/h \\
 & C)717km/h \\
 & D)400km/h \\
\end{align}\]

Answer 1

Hint: The magnitude and direction of velocity of plane A and direction of plane B are given. From this relative velocity of plane B with respect to A can be determined. Using these three velocities a vector diagram can be drawn. Using Lami’s theorem, we can equate these velocities and thereby we can determine the velocity of plane B.
Formula used:
\[{{\vec{v}}_{B/A}}={{\vec{v}}_{B}}-{{\vec{v}}_{A}}\]
\[\dfrac{{{{\vec{v}}}_{A}}}{\sin 75}=\dfrac{{{{\vec{v}}}_{B}}}{\sin 60}=\dfrac{{{{\vec{v}}}_{B/A}}}{\sin 45}\]

Complete step by step solution:
The relative velocity of B with respect to A is given by,
\[{{\vec{v}}_{B/A}}={{\vec{v}}_{B}}-{{\vec{v}}_{A}}\]
Where,
\[{{\vec{v}}_{A}}\]is the velocity of Plane A
\[{{\vec{v}}_{B}}\]is the velocity of Plane B
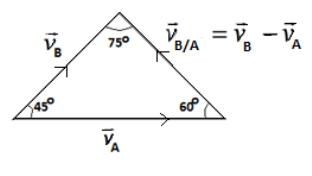
The vectors \[{{\vec{v}}_{B/A}}\], \[{{\vec{v}}_{B}}\]and \[{{\vec{v}}_{A}}\] make a triangle.

Given,
Velocity of plane A,\[{{v}_{A}}=800\hat{i}\]
According to Lami’s theorem,
\[\dfrac{{{{\vec{v}}}_{A}}}{\sin 75}=\dfrac{{{{\vec{v}}}_{B}}}{\sin 60}=\dfrac{{{{\vec{v}}}_{B/A}}}{\sin 45}\]
We have,
\[{{\vec{v}}_{B/A}}={{\vec{v}}_{B}}-{{\vec{v}}_{A}}\]
Substitute it in above equation , we get,
\[\dfrac{{{{\vec{v}}}_{A}}}{\sin 75}=\dfrac{{{{\vec{v}}}_{B}}}{\sin 60}=\dfrac{{{{\vec{v}}}_{B}}-{{{\vec{v}}}_{A}}}{\sin 45}\]
Then,
\[\dfrac{{{{\vec{v}}}_{A}}}{\sin 75}=\dfrac{{{{\vec{v}}}_{B}}}{\sin 60}\]
Substitute the value of \[{{\vec{v}}_{A}}\]in the above equation
\[{{\vec{v}}_{B}}=800\times \dfrac{\sin 60}{\sin 75}=717km/h\]

Therefore, the answer is option C.

Note:
Lami’s theorem relates the magnitudes of three concurrent, non-collinear and coplanar which keeps an object in static equilibrium, with the angles directly opposite to the corresponding vectors. According to the theorem,
 \[\dfrac{A}{\sin \alpha }=\dfrac{B}{\sin \beta }=\dfrac{C}{\sin \gamma }\]
Where A, B and C are the magnitudes of the three concurrent coplanar and noncollinear vectors \[{{\vec{v}}_{A}}\], \[{{\vec{v}}_{B}}\] and \[{{\vec{v}}_{C}}\]and α, β and γ are the angles directly opposite to the vectors.