Question

Parabolas are drawn to touch axes, which are inclined at an angle $\omega $ and all their directrices pass through a fixed point$\left( h,k \right)$. Prove that all parabolas touch the line
 \[\dfrac{x}{h+k\sec \omega }+\dfrac{y}{k+h\sec \omega }=1\]

Answer 1

Hint: We know that the equation of parabola where axes are inclined at any angle $\omega $ is $\sqrt{\dfrac{x}{a}}+\sqrt{\dfrac{y}{b}}=1$ where $a$ and $b$ are distances from the origin. We know the equation of the directory as $x\left( a+b\cos \omega \right)+y\left( b+\cos \omega \right)=ab\cos \omega $. We use them and prove that when the parabola touches the given line $\dfrac{x}{h+k\sec \omega }+\dfrac{y}{k+h\sec \omega }=1$ the points of contacts will have real $x$ and $y-$coordinates to prove the statement. \[\]

Complete step-by-step solution:
We know that parabola is the locus of a point which moves such that its distance from a fixed point is equal to its distance from a fixed-line. The fixed-line is called directrix and the fixed point is called the focus. We also know that the equation of the parabola with $a$ and $b$as the distance from the origin and any two axes without the restriction of the angle between them as right angle being the tangents is
\[\sqrt{\dfrac{x}{a}}+\sqrt{\dfrac{y}{b}}=1.....(1)\]
 

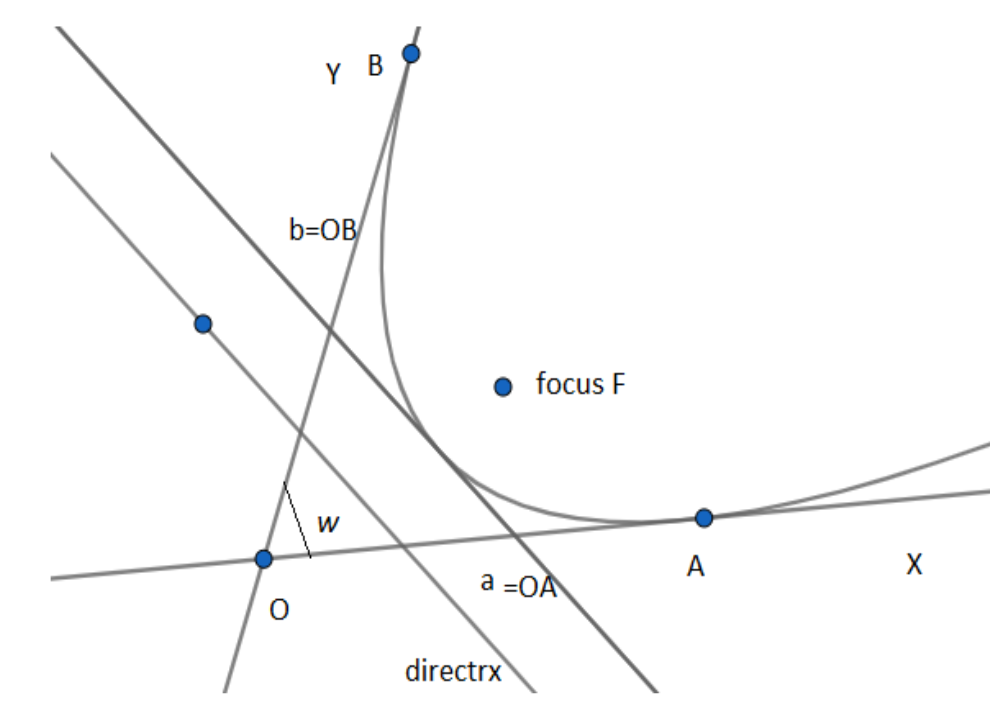
We know the equation of the directrix of the parabola where the axes are tangents and inclined to each other at an angle $\omega $ is given by,
\[x\left( a+b\cos \omega \right)+y\left( b+\cos \omega \right)=ab\cos \omega ....(2)\]
We are given that all directrices for different values of $\omega $ pass through a fixed point $\left( h,k \right)$. We put the point in equation of directrix and have
\[\begin{align}
  & h\left( a+b\cos \omega \right)+k\left( b+a\cos \omega \right)=ab\cos \omega \\
 & \Rightarrow ha+hb\cos \omega +kb+ka\cos \omega =ab\cos \omega \\
 & \Rightarrow h\left( b+k\sec \omega \right)+a\left( h\sec \omega +k \right)=ab...(3) \\
\end{align}\]
The equation of the given line is
\[\dfrac{x}{h+k\sec \omega }+\dfrac{y}{k+h\sec \omega }=1...(4)\]
We are asked to prove that parabola (1) touches the line(4). We can prove it by proving the converse of the statement that the line touches the parabola. If parabola touches the line we shall get two points of contact whose $x$and $y-$ordinates are going to be real. . We have from equation (1)
\[\sqrt{\dfrac{x}{a}}=1-\sqrt{\dfrac{y}{b}}=\dfrac{\sqrt{b}-\sqrt{y}}{\sqrt{b}}\]
We square both the sides to get,
\[\begin{align}
 &\dfrac{x}{a}=\dfrac{{{\left( \sqrt{b}-\sqrt{y} \right)}^{2}}}{b} \\
&\Rightarrow x=\dfrac{a}{b}{{\left( \sqrt{b}-\sqrt{y} \right)}^{2}}=\dfrac{a}{b}\left( b+y-2\sqrt{b}y \right) \\
\end{align}\]
We put $x$ it in equation (3) to get
\[\begin{align}
&\dfrac{a\left( b+y-2\sqrt{b}\sqrt{y} \right)}{b\left( h+k\sec \omega \right)}+\dfrac{y}{k+\sec \omega }=1 \\
 & \Rightarrow a\left( b+y-2\sqrt{b}\sqrt{y} \right)\left( k+h\sec \omega \right)+yb\left( h+k\sec \omega \right)=b\left( h+k\sec \omega \right)+k+\sec \omega \\
\end{align}\]
 We solve the above equation with the help of (3) and find that $y$ is a perfect square. Hence the parabola (1) touches the line. \[\]

Note: We note that $\omega $ cannot be the right angle here. While solving the problem from SL Loney’s book we need to know all the identities beforehand. The general equation of tangent at the point $\left( {{x}_{1}},{{y}_{1}} \right)$ to the parabola $\sqrt{\dfrac{x}{a}}+\sqrt{\dfrac{y}{b}}=1$ is $\dfrac{f}{a}+\dfrac{g}{b}=1$ where $f=\sqrt{a{{x}_{1}}},g=\sqrt{b{{y}_{1}}}$.