Question

P is a point on the ellipse \[\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1\] with foci at \[S.S'\]. Normal at P cuts the $x$-axis at G and if \[\dfrac{{SP}}{{S'P}} = \dfrac{2}{3}\] then \[\dfrac{{S'G}}{{SG}} = \]
A.\[\dfrac{4}{9}\]
B.\[\dfrac{2}{3}\]
C.\[\dfrac{{2a}}{{3b}}\]
D.\[\dfrac{3}{2}\]

Answer 1

Hint: Here, we will find the ratio of the distance of the point G from the focal points . We will use the distance between the focal points to find the length of the line segments from the ellipse. We will use the co-ordinates of the foci and the normal cuts the \[x\]-axis. By using the distance formula and then by substituting the value of the parametric co-ordinates, we will find the ratio of the distance of the point G from the focal points .

Formula Used:
We will use the following formula:
1.Distance between foci is given by the formula \[S'G + SG = 2ae\]
2.Distance on the major axis is given by the formula \[SP + S'P = 2a\]
3. \[d = \left| {\left( {{x_1} - {x_2}} \right) + \left( {{y_1} - {y_2}} \right)} \right|\]
4.The square of the sum of two numbers is given by the formula: \[{\left( {a + b} \right)^2} = {a^2} + {b^2} + 2ab\]
5.The square of the difference of two numbers is given by the formula: \[{\left( {a - b} \right)^2} = {a^2} + {b^2} - 2ab\]

Complete step-by-step answer:

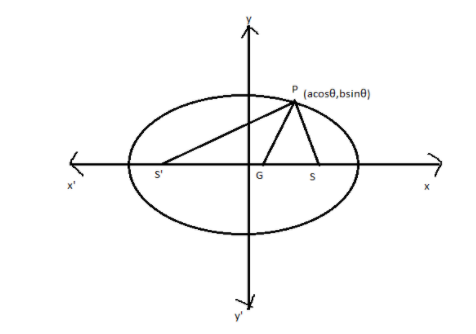
Let \[S'\] and \[S\] be the focal points and \[P\] be any point on the ellipse and \[G\] is the normal cutting the x-axis
Distance on the major axis is given by the formula \[SP + S'P = 2a\].
We are given that \[\dfrac{{SP}}{{S'P}} = \dfrac{2}{3}\]
So, we have
\[SP + S'P = 2 + 3 = 5\]
Thus, we get
\[\dfrac{{SP}}{{2a}} = \dfrac{2}{5}\]
On cross multiplication, we get
Thus, we get
\[\dfrac{{S'P}}{{2a}} = \dfrac{3}{5}\]
On cross multiplication, we get
\[ \Rightarrow S'P = \dfrac{{6a}}{5}\]
We know that \[SS' = 2ae\]
Let us consider \[\dfrac{{S'G}}{{SG}} = k\]
By adding \[\dfrac{{SG}}{{SG}}\] on both the sides, we get
\[ \Rightarrow \dfrac{{S'G}}{{SG}} + \dfrac{{SG}}{{SG}} = k + \dfrac{{SG}}{{SG}}\]
Now taking LCM, we get
\[ \Rightarrow \dfrac{{S'G + SG}}{{SG}} = k + 1\]
Substituting \[S'G + SG = 2ae\] in the above equation, we get
\[ \Rightarrow \dfrac{{2ae}}{{SG}} = k + 1\]
On cross multiplication, we get
\[ \Rightarrow SG = \dfrac{{2ae}}{{k + 1}}\] ……………………………………………………………………………………………\[\left( 1 \right)\]
Let \[P\left( {a\cos \theta ,b\sin \theta } \right)\] be a point on the ellipse \[\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1\].
Equation of Normal to the ellipse \[ax\sec \theta - by\cos ec\theta = {a^2} - {b^2}\] and intersects the \[x\]-axis at the point G.
By substituting \[y = 0\] in the equation of the normal, we get
\[ax\sec \theta = {a^2} - {b^2}\]
Dividing \[a\sec \theta \] on both sides, we get
\[ \Rightarrow x = \dfrac{{{a^2} - {b^2}}}{a} \cdot \dfrac{1}{{\sec \theta }}\]
Now using the reciprocal identity \[\dfrac{1}{{\sec \theta }} = \cos \theta \], we get
\[ \Rightarrow x = \dfrac{{{a^2} - {b^2}}}{a} \cdot \cos \theta \]
The co-ordinates of the Point G is \[\left( {\dfrac{{{a^2} - {b^2}}}{a} \cdot \cos \theta ,0} \right)\]
Let \[S\left( {ae,o} \right)\] and \[S'\left( { - ae,0} \right)\] be the co-ordinates on the ellipse.
Now, by using the distance formula \[d = \left| {\left( {{x_1} - {x_2}} \right) + \left( {{y_1} - {y_2}} \right)} \right|\], we get
\[\left| {ae - \dfrac{{{a^2} - {b^2}}}{a} \cdot \cos \theta } \right| = \dfrac{{2ae}}{{k + 1}}\]
 \[ \Rightarrow \left| {ae - a{e^2}\cos \theta } \right| = \dfrac{{2ae}}{{k + 1}}\]
By taking out the common factors, we get
\[ \Rightarrow ae\left( {1 - e\cos \theta } \right) = \dfrac{{2ae}}{{k + 1}}\]
\[ \Rightarrow \left( {1 - e\cos \theta } \right) = \dfrac{2}{{k + 1}}\]
\[ \Rightarrow 1 - \dfrac{2}{{k + 1}} = e\cos \theta \]………………………………………………………………………\[\left( 2 \right)\]
We have the equations of the lines as
\[ \Rightarrow {\left( { - ae - a\cos \theta } \right)^2} + {\left( {a\sin \theta } \right)^2} = {\left( {\dfrac{{6a}}{5}} \right)^2}\]
Now using the identity \[{\left( {a + b} \right)^2} = {a^2} + {b^2} + 2ab\], we get
\[ \Rightarrow {a^2}{e^2} + {a^2}{\cos ^2}\theta + 2{a^2}e\cos \theta + {a^2}{\sin ^2}\theta = \left( {\dfrac{{36{a^2}}}{{25}}} \right)\]
\[ \Rightarrow {a^2}{e^2} + {a^2} + 2{a^2}e\cos \theta = \left( {\dfrac{{36{a^2}}}{{25}}} \right)\] …………………………………………..\[\left( 3 \right)\]
\[ \Rightarrow {\left( {ae - a\cos \theta } \right)^2} + {\left( {a\sin \theta } \right)^2} = {\left( {\dfrac{{4a}}{5}} \right)^2}\]
Now using the identity \[{\left( {a - b} \right)^2} = {a^2} + {b^2} - 2ab\], we get
\[ \Rightarrow {a^2}{e^2} + {a^2}{\cos ^2}\theta - 2{a^2}e\cos \theta + {a^2}{\sin ^2}\theta = \left( {\dfrac{{16{a^2}}}{{25}}} \right)\]
\[ \Rightarrow {a^2}{e^2} + {a^2} - 2{a^2}e\cos \theta = \left( {\dfrac{{16{a^2}}}{{25}}} \right)\] …………………………………………..\[\left( 4 \right)\]
Subtracting equation \[\left( 4 \right)\]from equation \[\left( 3 \right)\], we get
\[ \Rightarrow - 2{a^2}e\cos \theta - 2{a^2}e\cos \theta = \left( {\dfrac{{36 - 16}}{{25}}} \right){a^2}\]
\[ \Rightarrow - 4{a^2}e\cos \theta = \left( {\dfrac{{20}}{{25}}} \right){a^2}\]
By cancelling the terms, we get
\[ \Rightarrow - e\cos \theta = \left( {\dfrac{1}{5}} \right)\]
\[ \Rightarrow \cos \theta = \left( { - \dfrac{1}{{5e}}} \right)\]
By substituting \[\cos \theta = \left( { - \dfrac{1}{{5e}}} \right)\] in equation \[\left( 2 \right)\], we get
\[ \Rightarrow 1 - \dfrac{2}{{k + 1}} = e\dfrac{{ - 1}}{{5e}}\]
\[ \Rightarrow 1 + \dfrac{1}{5} = \dfrac{2}{{k + 1}}\]
By taking the LCM, we get
\[ \Rightarrow 1 \times \dfrac{5}{5} + \dfrac{1}{5} = \dfrac{2}{{k + 1}}\]
\[ \Rightarrow \dfrac{6}{5} = \dfrac{2}{{k + 1}}\]
\[ \Rightarrow \dfrac{1}{{k + 1}} = \dfrac{3}{5}\]
On cross multiplication, we get
\[ \Rightarrow k + 1 = \dfrac{5}{3}\]
\[ \Rightarrow k = \dfrac{5}{3} - 1\]
By taking the LCM, we get
\[ \Rightarrow k = \dfrac{5}{3} - 1 \times \dfrac{3}{3}\]
\[ \Rightarrow k = \dfrac{{5 - 3}}{3}\]
\[ \Rightarrow k = \dfrac{2}{3}\]
Therefore, \[\dfrac{{S'G}}{{SG}} = \dfrac{2}{3}\].
Thus, option (B) is the correct answer.

Note: We know that the set of all points in a plane, the sum of whose distances from two fixed points in a plane is constant is an ellipse. These two fixed points are called the foci of the ellipse. The line joining the two foci of the ellipse is called the major axis of the ellipse and the line perpendicular to the major axis is called the minor axis of the ellipse. The endpoints of the ellipse are called the vertices of an ellipse.