Question

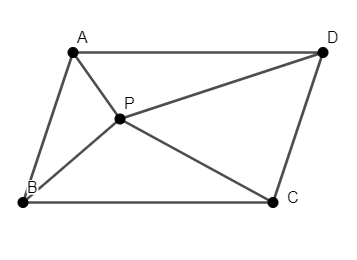
P is a point in the interior of a parallelogram ABCD. Show that \[ar\left( \Delta APB \right)+ar\left( \Delta PCD \right)=\dfrac{1}{2}ar\left( ABCD \right)\].

Answer 1

Hint: Draw a line EF parallel to line AB and CD passing through point P. Observe that AEFB and EDCF are parallelograms. Use the fact that if a parallelogram and triangle are on the same base, then the area of the triangle is half of the area of the parallelogram to prove the given equation.

Complete step-by-step solution -
We have a parallelogram ABCD and a point P inside the parallelogram. We have to prove that \[ar\left( \Delta APB \right)+ar\left( \Delta PCD \right)=\dfrac{1}{2}ar\left( ABCD \right)\].
Let’s draw a line EF parallel to line AB and CD passing through point P, as shown in the figure.

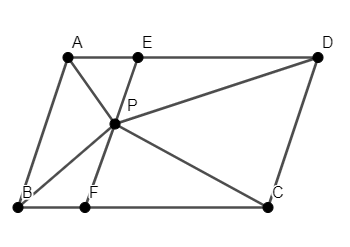
In quadrilateral AEFB, line AB is parallel to line EF due to construction and line AE is parallel to BF as ABCD is a parallelogram and opposite sides of a parallelogram are equal.
Thus, as $AB\parallel EF$ and $AE\parallel BF$, we observe that quadrilateral AEFB is a parallelogram.
Similarly, in quadrilateral EDCF, line EF is parallel to line CD due to construction and line ED is parallel to FC as ABCD is a parallelogram and opposite sides of a parallelogram are equal.
Thus, as $ED\parallel FC$ and $EF\parallel CD$, we observe that quadrilateral EDCF is a parallelogram.
Now, we know that the area of a triangle is half of the area of a parallelogram if they have the same base and parallels.
In parallelogram AEFB, we observe that $\Delta APB$ and parallelogram AEFB have the same base AB and are between the same set of parallel lines AB and EF.
Thus, we have $ar\left( \Delta APB \right)=\dfrac{1}{2}ar\left( AEFB \right).....\left( 1 \right)$.
Similarly, in parallelogram EDCF, we observe that $\Delta PCD$ and parallelogram EDCF have the same base CD and are between the same set of parallel lines EF and CD.
Thus, we have $ar\left( \Delta PCD \right)=\dfrac{1}{2}ar\left( EDCF \right).....\left( 2 \right)$.
Adding equation (1) and (2), we have $ar\left( \Delta APB \right)+ar\left( \Delta PCD \right)=\dfrac{1}{2}ar\left( AEFB \right)+\dfrac{1}{2}ar\left( EDCF \right).....\left( 3 \right)$ .
We observe that $ar\left( AEFB \right)+ar\left( EDCF \right)=ar\left( ABCD \right).....\left( 4 \right)$.
Substituting equation (4) in equation (3), we have $ar\left( \Delta APB \right)+ar\left( \Delta PCD \right)=\dfrac{1}{2}ar\left( AEFB \right)+\dfrac{1}{2}ar\left( EDCF \right)=\dfrac{1}{2}ar\left( ABCD \right)$.
Hence, we have proved that $ar\left( \Delta APB \right)+ar\left( \Delta PCD \right)=\dfrac{1}{2}ar\left( ABCD \right)$.

Note: It’s necessary to use the fact that the area of a triangle is half of the area of parallelogram if triangle and parallelogram have the same base and are between the same parallels. Otherwise, we won’t be able to prove the given statement.