Question

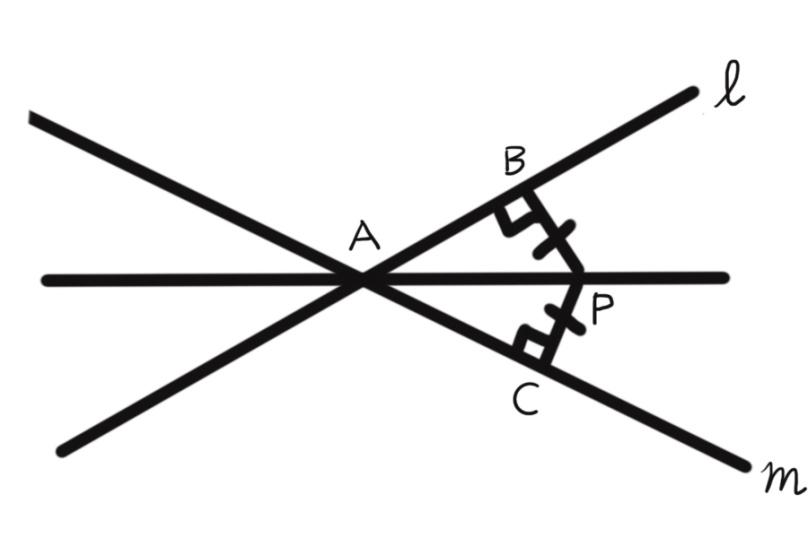
$P$ is a point equidistant from two lines $l$ and $m$ intersecting at point $A$. Show that the line $AP$ bisects the angle between them.

Answer 1

Hint: Notice that there are two right angled triangles in the diagram, $ABP$ and $ACP$. Start the solution by trying to prove that both are congruent to each other. For doing that you can use the HL(Hypotenuse-Leg) hypothesis. Once you have done that, you can easily show that $\angle BAP = \angle PAC$.

Complete step-by-step answer:
We can prove that $AP$ bisects the angle between $l$ and $m$ if we can show that the triangles $ABP$ and $ACP$ are congruent to each other. Notice that both these triangles are right angled triangles. And to prove congruence between two right angled triangles we use the HL(Hypotenuse-Leg) convention which states that that if the length of the hypotenuse and one of the other two legs of two right angled triangles are equal, then they are congruent to each other.
In the figure, it is shown that $AB = AC$. And we can also see that the hypotenuse $AP$ is common to both. That implies that both have the same length hypotenuse. Therefore, these two triangles are congruent by the HL hypothesis.
Now, we know that congruent triangles have equal sides and equal angles. Therefore, $\angle BAP = \angle PAC$ . This proves that $AP$ bisects the angle between $l$ and $m$.

Note: Remember that the HL(Hypotenuse-Leg) hypothesis is applicable only for right angled triangles. To tackle these sorts of problems, always start by proving that the two triangles are congruent. Once that is proven, you can easily show that the angle is bisected by the line because bisection of an angle basically means that we have to prove that the angle on both sides of the line are equal.