Question

P and Q are the point ${{t}_{1}},{{t}_{2}}$ on the parabola ${{y}^{2}}=4ax.$ If the normal at P, Q meet on parabola at $R\left( {{t}_{3}} \right),$ then ${{t}_{1}},{{t}_{2}}=2,{{t}_{3}}=-\left( {{t}_{1}}+{{t}_{2}} \right)$ and locus of midpoint of PQ is
$\left( a \right){{y}^{2}}=-2ax+4{{a}^{3}}$
$\left( b \right){{y}^{2}}=2ax+4{{a}^{2}}$
$\left( c \right){{y}^{2}}=-2ax+4{{a}^{2}}$
$\left( d \right){{y}^{2}}=-2ax$

Answer 1

Hint: Parametric coordinates on the parabola ${{y}^{2}}=4ax$ is given as $\left( a{{t}^{2}},2at \right)$ . Suppose P and Q as parametric coordinates in $'{{t}_{1}}','{{t}_{2}}'$ . Midpoint of a line joining $\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right)$ is given as n.
Suppose midpoint of PQ as variable (h, k) and try to eliminate ${{t}_{1}},{{t}_{2}},{{t}_{3}}$ with the help of given relations in the question.

Complete step-by-step answer:
As we know parametric coordinates on parabola ${{y}^{2}}=4ax$ can be given as $\left( a{{t}^{2}},2at \right)$ . So, the point P and Q on the parabola ${{y}^{2}}=4ax$ can be given as $\left( at_{1}^{2},2a{{t}_{1}} \right),\left( at_{2}^{2},2a{{t}_{2}} \right).$
Because P and Q are given as ${{t}_{1}},{{t}_{2}}$ on the parabola w.r.t parametric coordinates. And similarly, the point R can be given as $\left( at_{3}^{2},2a{{t}_{3}} \right)$ as R is given as $'{{t}_{3}}'$ in the problem. And we know relation in ${{t}_{1}},{{t}_{2}},{{t}_{3}}$ as
$\begin{align}
  & {{t}_{1}}{{t}_{2}}=2.................\left( i \right) \\
 & {{t}_{3}}=-\left( {{t}_{1}}+{{t}_{2}} \right)...........\left( ii \right) \\
\end{align}$
So, we can draw diagram with the above information as

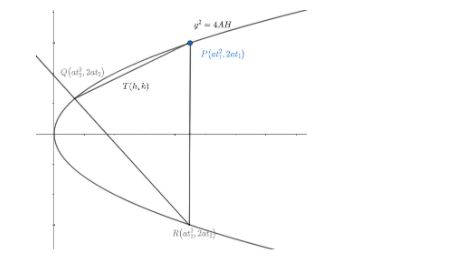
Now, we know that mid-point of point $\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right)$ can be given as
$\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)$
So, point T i.e. mid-point of P and Q can be given as
$\begin{align}
  & \left( \dfrac{at_{{}}^{{}}+at_{2}^{2}}{2},\dfrac{2a{{t}_{1}}+2a{{t}_{2}}}{2} \right) \\
 & \Rightarrow \left( \dfrac{a\left( t_{1}^{2}+t_{2}^{2} \right)}{2},a\left( {{t}_{1}}+{{t}_{2}} \right) \right) \\
\end{align}$
So, we can equate these coordinates to (h, k) as we have supposed the point T as (h, k). So, we get
$h=\dfrac{a\left( t_{1}^{2}+t_{2}^{2} \right)}{2},k=a\left( {{t}_{1}}+{{t}_{2}} \right)$
As, we know the algebraic identity of ${{\left( a+b \right)}^{2}}$ is given as
$\begin{align}
  & {{\left( a+b \right)}^{2}}={{a}^{2}}+{{b}^{2}}+2ab+ \\
 & \Rightarrow {{a}^{2}}+{{b}^{2}}={{\left( a+b \right)}^{2}}-2ab \\
\end{align}$
So, we can replace $t_{1}^{2}+t_{2}^{2}$ from $h=\dfrac{a\left( t_{1}^{2}+t_{2}^{2} \right)}{2}$ in the above equation by ${{\left( {{t}_{1}}+{{t}_{2}} \right)}^{2}}-2{{t}_{1}}{{t}_{2}}$ , with the help of equation (viii) . So we get
$h=\dfrac{a\left[ {{\left( {{t}_{1}}+{{t}_{2}} \right)}^{2}}-2{{t}_{1}}{{t}_{2}} \right]}{2},k=a\left[ {{t}_{1}}+{{t}_{2}} \right]$
Put ${{t}_{1}}+{{t}_{2}}=-{{t}_{3}},{{t}_{1}}{{t}_{2}}=2$ from the equation (i) and (ii). So, we get values of h and K as
$\begin{align}
  & h=\dfrac{a\left[ {{\left( -{{t}_{3}} \right)}^{2}}-2\times 2 \right]}{2},k=-{{t}_{3}}a \\
 & h=\dfrac{a\left( t_{3}^{2}-4 \right)}{2},k=-{{t}_{3}}a \\
\end{align}$
Now, we can eliminate ${{t}_{3}}$ by putting value of ${{t}_{3}}$ from the equation
$k=-{{t}_{3}}a\Rightarrow {{t}_{3}}=\left( \dfrac{-k}{a} \right)$
To the equation
$h=\dfrac{a\left( t_{3}^{2}-4 \right)}{2}$
So, we get equation a line passes through $\left( {{x}_{1}},{{y}_{1}} \right)$ with slope m is
$\begin{align}
  & y-{{y}_{1}}=m\left( x-{{x}_{1}} \right) \\
 & h=\dfrac{a}{2}\left( {{\left( \dfrac{-k}{a} \right)}^{2}}-4 \right) \\
 & h=\dfrac{a}{2}\left( \dfrac{{{k}^{2}}}{{{a}^{2}}}-4 \right) \\
 & h=\dfrac{a}{2}\left( \dfrac{{{k}^{2}}-4{{a}^{2}}}{{{a}^{2}}} \right) \\
 & \dfrac{h}{1}=\dfrac{{{k}^{2}}-4{{a}^{2}}}{2a} \\
\end{align}$
On cross multiplying the above equation, we get
$\begin{align}
  & 2ah={{k}^{2}}-4{{a}^{2}} \\
 & \Rightarrow {{k}^{2}}=2ah+4{{a}^{2}} \\
\end{align}$
Now, we can replace (h, k) by (x, y) to get the required locus
${{y}^{2}}=2ax+4{{a}^{2}}$

So, the correct answer is “Option b”.

Note: Don’t need to calculate any equation of normal or tangent. Just use only the midpoint concept for two points on a line. Suppose the coordinates of P and Q as
$\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right)$
Use only parametric coordinates as specified in the problem. One may confuse the statement that how to normal can be drawn from one point. So, we should know that there are a maximum of three that can be drawn from one point. As equation of normal for parabola is
$tx+y-2at-a{{t}^{3}}=0$
Which is a cubic equation in ‘t’ , so there are 3 roots of the above equation and hence 3 normal can be possible from one point.