Question

P and Q are respectively the midpoints of sides AB and BC of a triangle ABC and R is the midpoint of AP. So prove that $ar\left( PRQ \right)=\dfrac{1}{2}ar\left( ARC \right)$.

Answer 1

Hint: To solve this question, we need to use the theorem of median which states that a median divides a triangle into two triangles of equal areas. By using this theorem, we can relate the areas of the smaller triangles PQR and ARC to the area of the bigger triangle ABC. From these two relations, we can derive the required relation, which is given in the above question.

Complete step by step solution:
From the information given in the above question, we can draw the triangle ABC as shown in the below figure.

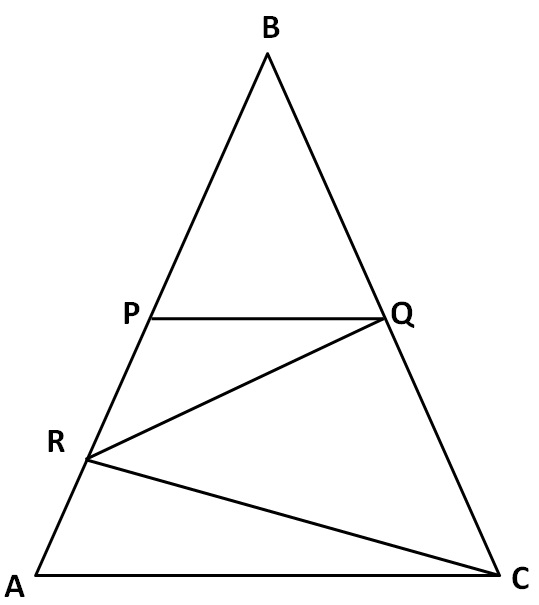
Now, let us join the points AQ and CP as shown in the below figure.

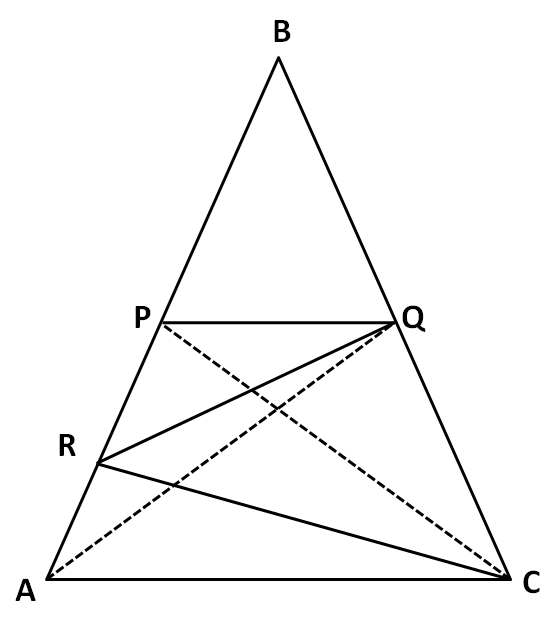
Now, let us observe the triangle APQ. Since R is given to be the midpoint of AP, we can say that QR is the median of the triangle APQ.
Now, we know that a median divides a triangle into two triangles of equal areas. This means we can write
$\Rightarrow ar\left( PRQ \right)=\dfrac{1}{2}ar\left( APQ \right).......\left( i \right)$
Similarly, in the triangle AQB we can observe that QP is a median. Therefore, we can write
$\Rightarrow ar\left( APQ \right)=\dfrac{1}{2}ar\left( AQB \right).......\left( ii \right)$
Now, in the triangle ABC, since AQ is the median we can write
$\Rightarrow ar\left( AQB \right)=\dfrac{1}{2}ar\left( ABC \right).......\left( iii \right)$
Putting the equation (ii) in (ii) we get
$\begin{align}
  & \Rightarrow ar\left( APQ \right)=\dfrac{1}{2}\times \dfrac{1}{2}ar\left( ABC \right) \\
 & \Rightarrow ar\left( APQ \right)=\dfrac{1}{4}ar\left( ABC \right).......\left( iv \right) \\
\end{align}$
Substituting the equation (iv) in (i) we get
\[\begin{align}
  & \Rightarrow ar\left( PRQ \right)=\dfrac{1}{2}\times \dfrac{1}{4}ar\left( ABC \right) \\
 & \Rightarrow ar\left( PRQ \right)=\dfrac{1}{8}ar\left( ABC \right).......\left( vi \right) \\
\end{align}\]
Now, in the triangle APC, CR is the median. Therefore we can write
$\Rightarrow ar\left( ARC \right)=\dfrac{1}{2}ar\left( APC \right)........\left( vii \right)$
Since CP is the median in the triangle ABC, we can write
$\Rightarrow ar\left( APC \right)=\dfrac{1}{2}ar\left( ABC \right).......\left( viii \right)$
Putting the equation (viii) in (vii) we get
$\begin{align}
  & \Rightarrow ar\left( ARC \right)=\dfrac{1}{2}\times \dfrac{1}{2}ar\left( ABC \right) \\
 & \Rightarrow ar\left( ARC \right)=\dfrac{1}{4}ar\left( ABC \right)........\left( ix \right) \\
\end{align}$
Dividing the equation (vi) by the equation (ix) we get
$\begin{align}
  & \Rightarrow \dfrac{ar\left( PRQ \right)}{ar\left( ARC \right)}=\dfrac{\dfrac{1}{8}ar\left( ABC \right)}{\dfrac{1}{4}ar\left( ABC \right)} \\
 & \Rightarrow \dfrac{ar\left( PRQ \right)}{ar\left( ARC \right)}=\dfrac{4}{8} \\
 & \Rightarrow \dfrac{ar\left( PRQ \right)}{ar\left( ARC \right)}=\dfrac{1}{2} \\
 & \Rightarrow ar\left( PRQ \right)=\dfrac{1}{2}ar\left( ARC \right) \\
\end{align}$

Note: There is no direct relation between the triangles PQR and ARC. That’s why we have related their areas to the area of a common triangle, which is the triangle ABC. There must be no mistake while finding the median in a triangle. For this, we can focus on the definition of a median. A median is defined as the line joining a vertex and the midpoint of the side opposite to the vertex.