Question

\[\overset{\to }{\mathop{a}}\,,\overset{\to }{\mathop{b}}\,,\overset{\to }{\mathop{c}}\,\] are those non – coplanar vectors. Then the equation, \[\overset{\to }{\mathop{r}}\,=\left( 1-p-q \right)\overset{\to }{\mathop{a}}\,+p\overset{\to }{\mathop{b}}\,+q\overset{\to }{\mathop{c}}\,\] represents:
(a) A straight line
(b) A plane
(c) A plane passing through the origin
(d) A sphere

Answer 1

Hint:\[\overset{\to }{\mathop{a}}\,,\overset{\to }{\mathop{b}}\,\] and \[\overset{\to }{\mathop{c}}\,\] are non –coplanar vectors, represent them in 3D. Take each option, compare the equation given and draw figure and find out what the equation represents.

Complete step-by-step answer:
It is given to us that \[\overset{\to }{\mathop{a}}\,,\overset{\to }{\mathop{b}}\,,\overset{\to }{\mathop{c}}\,\] are 3 non – planar vectors, which means that these 3 vectors \[\overset{\to }{\mathop{a}}\,,\overset{\to }{\mathop{b}}\,\] and \[\overset{\to }{\mathop{c}}\,\] doesn’t lie on the same plane.
Now given to us the equation,
\[\overset{\to }{\mathop{r}}\,=\left( 1-p-q \right)\overset{\to }{\mathop{a}}\,+p\overset{\to }{\mathop{b}}\,+q\overset{\to }{\mathop{c}}\,........(1)\]
Now we need to find what this equation represents.
We can first look into an example of non – coplanar vector \[\overset{\to }{\mathop{a}}\,,\overset{\to }{\mathop{b}}\,\] and \[\overset{\to }{\mathop{c}}\,\].
Now x – axis, y – axis and z – axis, they are all \[{{90}^{\circ }}\] from each other.

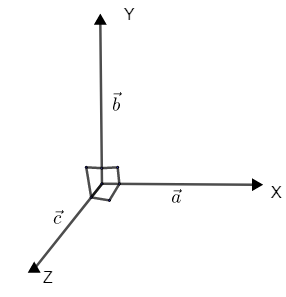
Let us consider first a straight line. Now, non – coplanar vectors doesn’t lie on the same plane, thus they cannot represent a straight line. Thus equation (1) doesn’t represent a straight line.
Now we need to check if equation (1) represents a plane.
Now let's draw the figure as given. Now it became a plane which consists of all the three vectors. Thus we can say that the equation represents a plane.

Now let us check with the other option. Now this plane is represented in the three dimensions.
Thus it doesn’t pass through the origin i.e. the plane doesn’t pass through the origin. By comparing the figure and equation (1), it can never represent a sphere.
Thus the equation, \[\overset{\to }{\mathop{r}}\,=\left( 1-p-q \right)\overset{\to }{\mathop{a}}\,+p\overset{\to }{\mathop{b}}\,+q\overset{\to }{\mathop{c}}\,\] represents a plane.
\[\therefore \] Option (b) is the correct answer.

Note: If two vectors are coplanar, then they will lie on the same plane i.e. two vectors are parallel to the xy plane or any plane, they are coplanar. If the given vectors lie in the same line, then they are collinear.