Question

Out of 150 students who read newspapers at least one of newspapers; The Times of India, The Hindustan Times, and The Hindu, there are 65 who read The Times of India, 41 who read The Hindu and 50 who read The Hindustan Times. What is the maximum possible number of students who read all three newspapers?
A. 7
B. 42
C. 3
D. Cannot be determined

Answer 1

Hint: Let the number of students who read all the newspapers be $x$. Since, we have to find the maximum value of $x$, then there is no student who reads only 2 newspapers. Hence, determine the number of students who read only one newspaper. Then use the condition that there are a total 150 students to find the value of $x$.

Complete step-by-step answer:
Here, we are given that the number of students who read the newspapers is 150.
We have to find the maximum possible number of students who read all the three newspapers.
Then, we will assume, there is no student who reads only 2 newspapers.
That is either a student reads only one newspaper or he reads all the newspapers.
Let the number of students who read all the newspaper be $x$, then the students who read only The Times of India be $65 - x$ , the number of students who read only The Hindustan Times be $50 - x$ and the students who read only The Hindu be $41 - x$.
We will represent the above information in a Venn-diagram.

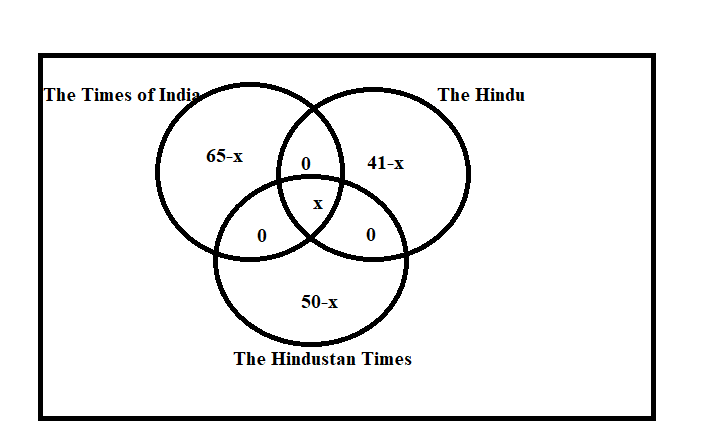
Also, We are given that there are a total of 150 students.
This implies,
$65 - x + 50 - x + 41 - x + x = 150$
On solving the above equation, we will get,
$
  65 + 50 + 41 - 2x = 150 \\
   \Rightarrow 156 - 2x = 150 \\
   \Rightarrow 2x = 6 \\
$
On dividing the equation by 2, we will get,
$x = 3$
Therefore, there can be a maximum of three students who read all the three newspapers.
Hence, option C is correct.

Note: Many students by ignoring the word maximum in the above question. They find the data incomplete and select option D which is incorrect. A Venn-diagram helps us to understand the problem in a better way. But, this question can also be done by using the formula, $n\left( {A \cup B \cup C} \right) = n\left( A \right) + n\left( B \right) + n\left( C \right) - n\left( {A \cap B} \right) - n\left( {B \cap C} \right) - n\left( {A \cap C} \right) + n\left( {A \cap B \cap C} \right)$