Question

Out of 100 students, 15 passed in English, 12 passed in Mathematics, 8 in Science, 6 in English & Mathematics, 7Mathematics and Science, 4 English & Science, 4 in all the three. Find how many passes
 

1.In English & Mathematics but not in Science
2.In Mathematics & Science but not in English
3.In only Mathematics
4.In more than one subject only

Answer 1

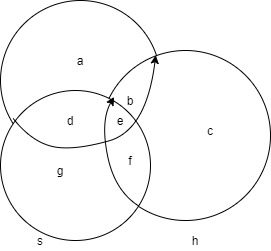
Hint: Draw Venn-diagram for three sets, start from all three regions then complete for two common sets then thirdly for the full set also label the regions so that we can easily solve the questions in different questions in different parts.
Formula used:
1.$n\left( AuBuC \right)=n\left( A \right)+n\left( B \right)+n\left( C \right)=n\left( A\bigcap B \right)-n\left( B\bigcap C \right)-n\left( A\bigcap C \right)+n\left( A\bigcap B\bigcap C \right)$
2.$\text{Number of students studying English }\!\!\And\!\!\text{ Maths but not science}=n\left( E\bigcap M \right)-n\left( E\bigcap M\bigcap S \right)$
3.$\text{Number}$ $\text{Math }\!\!\And\!\!\text{ Science but not English}=n\left( M\bigcap S \right)-n\left( E\bigcap M\bigcap S \right)$
4.$\text{No of students study only Mathematics}=n\left( E\bigcap M \right)-n\left( S\bigcap M \right)+n\left( E\bigcap M\bigcap B \right)$
5.$\text{More than one subject}=n\left( E\bigcap M \right)+n\left( E\bigcap S \right)-n\left( E\bigcap M\bigcap S \right)$

Complete step-by-step answer:

$\begin{align}
  & \text{Total number of students}=100 \\
 & \text{ Number of students }n\left( E \right)=15 \\
 & \text{ }n\left( M \right)=12 \\
 & \text{ }n\left( S \right)=8 \\
\end{align}$
     $\begin{align}
  & \text{ }E\text{ and }M\text{ }n\left( E\bigcap M \right)=6 \\
 & \text{ }n\left( M\bigcap S \right)=7 \\
 & \text{ }n\left( E\bigcap S \right)=4 \\
 & \text{ }n\left( E\bigcap S\bigcap M \right)=4 \\
\end{align}$
\[\begin{align}
  & n\left( E\bigcap S\bigcap M \right)=n\left( E \right)+n\left( S \right)+n\left( M \right)-n\left( E\bigcap S \right) \\
 & \text{ }-n\left( S\bigcap M \right)-n\left( M\bigcap E \right)+n\left( M\bigcap E\bigcap S \right) \\
\end{align}\]
\[\begin{align}
  & =15+12+8-4-7-6+4 \\
 & \text{ }=22 \\
\end{align}\]
$\begin{align}
  & \text{Number of students those who study either of the three subjects}=22 \\
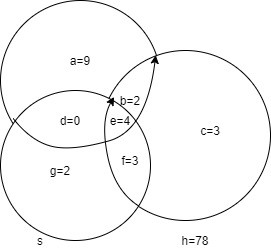
 & a+b+c+d+e+f+g=22 \\
 & \text{Therefore number of students those who study none of the subject}=100-22 \\
 & \text{ }=78 \\
 & \text{ }=h \\
\end{align}$
$\text{Number of students study English }\!\!\And\!\!\text{ Mathematics but not Science}=n\left( E\bigcap M \right)-n\left( E\bigcap M\bigcap S \right)$
$\begin{align}
  & =\text{Number of students studyingstuding English }\!\!\And\!\!\text{ Mathematics}-\text{Number of students studyingstuding all three subjects}\text{.} \\
 & \text{=6}-4 \\
 & =2 \\
\end{align}$
$\text{Number of studentsos students studying Mathematics }\!\!\And\!\!\text{ Science but not English}=n\left( M\bigcap S \right)-n\left( M\bigcap S\bigcap E \right)$ $\begin{align}
  & =7-4 \\
 & =3 \\
\end{align}$
\[\text{Number of students studying Only Mathematics}=n\left( M \right)-n\left( M\bigcap E \right)-n\left( M\bigcap E \right)+n\left( M\bigcap S\bigcap E \right)\] \[\begin{align}
  & =12-\text{6}-7+4 \\
 & =3 \\
\end{align}\]
\[\text{Number of students studying more than one subject}=n\left( M\bigcap S \right)+n\left( S\bigcap E \right)+n\left( E\bigcap M \right)-2\left( E\bigcap M\bigcap S \right)\]
$\begin{align}
  & =6+7+4-2\times \left( 4 \right) \\
 & =17-8=9 \\
\end{align}$
Note: We can plot the values of a, b, c, d, e, f, g & h orally. We start with placing the values of e by i.e. common region of all three subjects. After this we can find the value of e, d and f i.e. common region for two subjects then we calculate a, g, c the region for one subject and finally we can calculate h by subtracting from total$-\left( \text{a}+\text{b}+\text{c}+\text{d}+\text{e}+\text{f}+\text{g} \right)$ .