Question

Oscar’s dog house is shaped like a tent as shown to the right. The slanted sides are both $5\,m$ long and the bottom of the house is $6\,m$ across. What is the height of this doghouse?

Answer 1

Hint: Here, we are given both the slanted sides and bottom side value. And we need to find the height of the tent. The Pythagoras theorem is a mathematical law that states that the sum of squares of the lengths of the two short sides of the right triangle is equal to the square of the length of the hypotenuse. We will use the Pythagoras theorem to get the final output.

Complete step by step answer:
Given that, the slanted sides are $5\,m$ and the bottom side is $6\,m$. According to the diagram given and the information, we have,

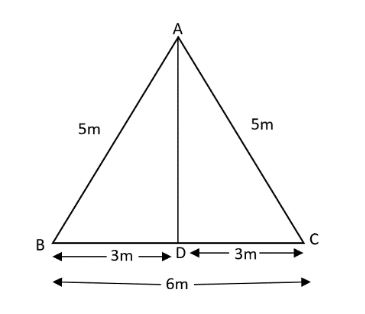
Here, AC = AB = $5\,m$ (given)
BC = $6\,m$ (given)
Since, \[BC = AD + DC\]
\[AD = DC = 3m\]
We will use the Pythagoras theorem to find the height (i.e. AD) of this tent as shown below:
\[A{C^2} = A{D^2} + D{C^2}\]
Substituting the values we will get,
\[ \Rightarrow {5^2} = A{D^2} + {3^2}\]
Using the transposing method, we will move one RHS term to LHS, we will get,
\[ \Rightarrow {5^2} - {3^2} = A{D^2}\]
Rearranging both the sides, we will get,
\[ \Rightarrow A{D^2} = {5^2} - {3^2}\]
\[ \Rightarrow A{D^2} = 25 - 9\]
On evaluating this, we will get,
\[ \Rightarrow A{D^2} = 16\]
\[ \Rightarrow AD = \sqrt {16} \]
\[ \therefore AD = 4\,m\]

Hence, the height of his doghouse is 4 m.

Note: As we know that, for using the Pythagorean Theorem, the triangle should be a right angled triangle. It gives a fundamental relation among the three sides of a right triangle. Thus, this equation relates the sides of a right triangle in a simple way, so that if the lengths of any two sides are known the length of the third side can be found out.