Question

What is the ordered pair that satisfies the equation \[3x + 4y = 24\]?

Answer 1

Hint: We know that a first degree equation in x and y, \[ax + by + c = 0\] always represents a straight line. This form is known as the general form of straight line.
Formula used: From the general form of straight line, \[ax + by + c = 0\], we know that
> Slope of this line \[ = - \dfrac{a}{b} = - \dfrac{{coeff.of(x)}}{{coeff.of(y)}}\]
> Intercept by this line on x-axis\[ = - \dfrac{c}{a}\]
> Intercept by this line on y-axis\[ = - \dfrac{c}{b}\]
Given: Equation \[3x + 4y = 24\]
To find: Ordered pair that satisfy the given equation, \[3x + 4y = 24\]

Complete step-by-step solution:
Step 1: Conversion of given equation into its general form of equation
We know that the general form of straight line is given by the equation,
\[ax + by + c = 0\]
Now, rearranging the terms of the given equation \[3x + 4y = 24\],
Taking $24$on the left hand side of the equation, we get
\[ \Rightarrow \]\[3x + 4y = 24\]
\[ \Rightarrow \]\[3x + 4y - 24 = 0\] (Given equation is now converted into general form of straight line)
Step 2: comparing equations \[3x + 4y = 24\]& \[ax + by + c = 0\] both, we get
\[ \Rightarrow \]\[ax + by + c = 0\]
\[ \Rightarrow \]\[3x + 4y = 24\]
\[ \Leftrightarrow \]\[a = 3,b = 4\& c = - 24\]
Step 3: Finding the ordered pair that satisfy the given equation,
Now, from general form of straight line i.e. \[ax + by + c = 0\], we know that
1) Intercept by this line on x-axis \[ = - \dfrac{c}{a}\]
Substituting the values of a & c we get,
Intercept by this line on x-axis \[ = - \dfrac{{( - 24)}}{3} = 8\]& since this intercept is only on x-axis therefore, \[y = 0\]
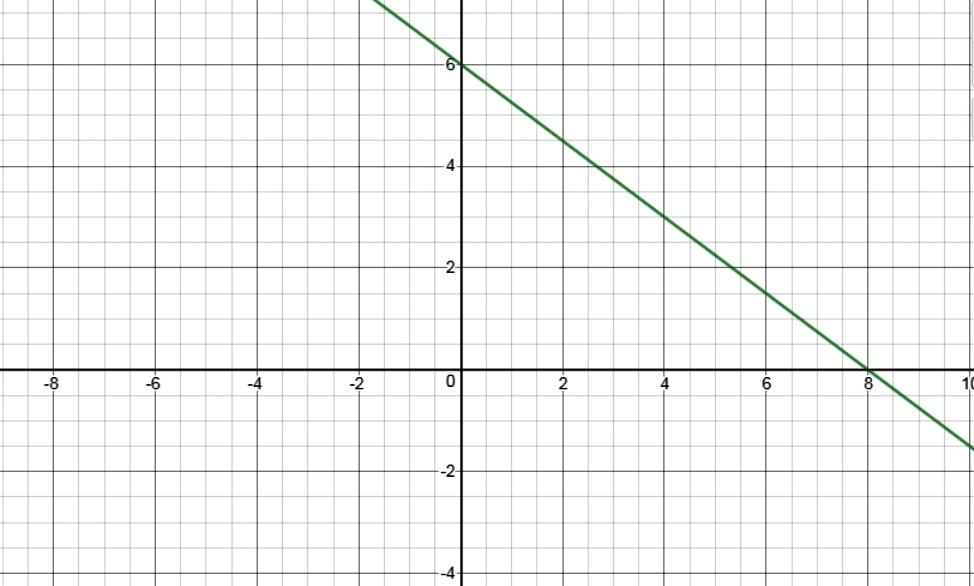
So, \[(8,0)\]is a point that satisfy the equation \[3x + 4y = 24\]
2) Intercept by this line on y-axis\[ = - \dfrac{c}{b}\]
Substituting the values of b & c we get,
Intercept by this line on y-axis \[ = - \dfrac{{( - 24)}}{4} = 6\]& since this intercept is only on y-axis therefore, \[x = 0\]
So, \[(0,6)\] is a point that satisfy the equation \[3x + 4y = 24\]
Hence, \[(8,0)\]&\[(0,6)\]are the ordered pairs that satisfies the equation \[3x + 4y = 24\].

Note: Here we need to remember few important properties of straight line.
> Equation of line parallel to line \[ax + by + c = 0\] is, \[ax + by + \lambda = 0\]
> Equation of line perpendicular to line \[ax + by + c = 0\] is, \[bx - ay + k = 0\]
Here \[\lambda \], \[k\] are parameters and their values are obtained with the help of additional information given in the problem.