Question

One side of a parallelogram is 18 cm and its distance from the opposite side is 8 cm. The area of the parallelogram is:
A) $48\mathop {{\rm{ }}cm}\nolimits^2 $
B) \[72\mathop {{\rm{ }}cm}\nolimits^2 \]
C) $100\mathop {{\rm{ }}cm}\nolimits^2 $
D) $144\mathop {{\rm{ }}cm}\nolimits^2 $

Answer 1

Hint: The parallelogram is a quadrilateral whose opposite sides are parallel to each other. The angle between two adjacent sides of parallelogram is not equal to $90^\circ $ (i.e. $ \ne 90^\circ $)
Area of the parallelogram is equal to the multiplication of base and height.
Area of parallelogram = base $ \times $height
Base is the side of the parallelogram on which height is drawn. Height is the distance between the base side and the side opposite to it.

Complete step by step solution:
Step 1

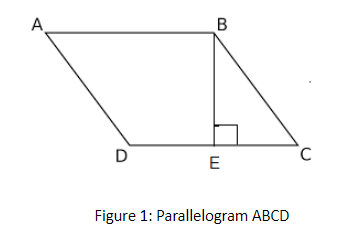
Step 2
Length AB = 18 $cm$ (given)

Step 3
Length AB distance from its opposite side (i.e. side CD) is 8 $cm$. (given)
$ \Rightarrow $ Distance between sides AB and CD = 8 $cm$ …… (1)

Step 4
Distance between sides AB and CD is BE
$\therefore $ Height BE = 8 $cm$ (from (1))

Step 5
Area of parallelogram = base $ \times $height
                                        \[\begin{array}{l}
 = {\rm{ }}18{\rm{ }} \times {\rm{ }}8\\
 = {\rm{ }}144{\rm{ }}\mathop {cm}\nolimits^2
\end{array}\]

The area of parallelogram is 144 $\mathop {cm}\nolimits^2 $. The correct option is (D).

Note:
The height always falls perpendicular to the side from the vertex it is measured. The opposite sides of a parallelogram are equal in length, but their diagonals are not equal.
Diagonals of a parallelogram bisect each other.
Length is represented in $units$ (example given: $cm$).
Area is represented in $sq.{\rm{ }}units$(example given: \[\mathop {cm}\nolimits^2 \])
Volume is represented in $cubic{\rm{ }}units$ (example given: \[\mathop {cm}\nolimits^3 \])