Question

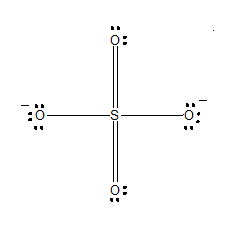
One of the resonating structures of $SO_4^{ - 2}$ is as shown. Which set of formal charge on oxygen and bond order is correct?

(A) -0.5 and 1.5
(B) 1.5 and 3
(C) 2 and 3
(D) 1.5 and 1.5

Answer 1

Hint: To solve this question we should know the formula to calculate set formal charge and bond order as well as the theory behind it. The formal charge on oxygen in $SO_4^{ - 2}$ is equal to the formal charge on each oxygen and takes an average of all.

Complete step by step answer:
The formal charge is the number of charges on an atom in a molecule, under assumption that electrons in all bonds are equally shared irrespective of the relative electronegativity.
Formula of formal charges:
\[Formal{\text{ }}charge{\text{ }} = {\text{ }}number{\text{ }}of{\text{ }}valence{\text{ }}electron{\text{ }}in{\text{ }}free{\text{ }}atom{\text{ }} - {\text{ }}number{\text{ }}of{\text{ }}lone{\text{ }}pair{\text{ }}electrons{\text{ }} - {\text{ }}\dfrac{1}{2}number{\text{ }}of{\text{ }}bond{\text{ }}pair{\text{ }}electrons.\]

Carefully refer to the diagram, where each oxygen is numbered.
-The formal charges of oxygen 1:
\[Formal{\text{ }}charge{\text{ }} = {\text{ }}number{\text{ }}of{\text{ }}valence{\text{ }}electron{\text{ }}in{\text{ }}free{\text{ }}atom{\text{ }} - {\text{ }}number{\text{ }}of{\text{ }}lone{\text{ }}pair{\text{ }}electrons{\text{ }} - {\text{ }}\dfrac{1}{2}number{\text{ }}of{\text{ }}bond{\text{ }}pair{\text{ }}electrons.\]
= 6 - 4 - 2
  = 0
-The formal charges of oxygen 2:
\[Formal{\text{ }}charge{\text{ }} = {\text{ }}number{\text{ }}of{\text{ }}valence{\text{ }}electron{\text{ }}in{\text{ }}free{\text{ }}atom{\text{ }} - {\text{ }}number{\text{ }}of{\text{ }}lone{\text{ }}pair{\text{ }}electrons{\text{ }} - {\text{ }}\dfrac{1}{2}number{\text{ }}of{\text{ }}bond{\text{ }}pair{\text{ }}electrons.\]
= 6 - 6 - 1
  = -1
 -The formal charges of oxygen 3:
\[Formal{\text{ }}charge{\text{ }} = {\text{ }}number{\text{ }}of{\text{ }}valence{\text{ }}electron{\text{ }}in{\text{ }}free{\text{ }}atom{\text{ }} - {\text{ }}number{\text{ }}of{\text{ }}lone{\text{ }}pair{\text{ }}electrons{\text{ }} - {\text{ }}\dfrac{1}{2}number{\text{ }}of{\text{ }}bond{\text{ }}pair{\text{ }}electrons.\]
= 6 - 4 - 2
  = 0

-The formal charges of oxygen 4:
\[Formal{\text{ }}charge{\text{ }} = {\text{ }}number{\text{ }}of{\text{ }}valence{\text{ }}electron{\text{ }}in{\text{ }}free{\text{ }}atom{\text{ }} - {\text{ }}number{\text{ }}of{\text{ }}lone{\text{ }}pair{\text{ }}electrons{\text{ }} - {\text{ }}\dfrac{1}{2}number{\text{ }}of{\text{ }}bond{\text{ }}pair{\text{ }}electrons.\]
 = 6 - 6 - 1
 = -1
The total formal charges on oxygen in $SO_4^{ - 2}$ is:

\[Formal{\text{ }}charges{\text{ }}in{\text{ }}oxygen{\text{ }} = \;\;\dfrac{{sum{\text{ }}of{\text{ }}formal{\text{ }}charge{\text{ }}on{\text{ }}oxygen{\text{ }}1,2,3{\text{ }}and{\text{ }}4}}{{Total{\text{ }}number{\text{ }}of{\text{ }}oxygen}}\]
   \[ = \dfrac{{0 + ( - 1) + 0 + ( - 1)}}{4}\]
    = - 0.5
Thus, formal charge on $SO_4^{ - 2}$ is - 0.5

Bond order is the number of chemical bonds present between the pairs of atoms
\[bond{\text{ }}order = \dfrac{{number{\text{ }}of{\text{ }}bonds}}{{Total{\text{ }}number{\text{ }}of{\text{ }}atom{\text{ }}sharing{\text{ }}the{\text{ }}bond}}\]
  \[ = \dfrac{6}{4}\]
  = 1.5
So, the correct answer is “Option A”.

Note: Generally, Formula to calculate bond pair:
\[Bond{\text{ }}order{\text{ }} = \dfrac{1}{2}({N_b} - {N_a})\]
Where, ${N_b}$ = number of bonding electrons
             ${N_a}$ = number of antibonding electrons
But for compound that has resonating structures, then the formula will be
\[bond{\text{ }}order = \dfrac{{number{\text{ }}of{\text{ }}bonds}}{{Total{\text{ }}number{\text{ }}of{\text{ }}atom{\text{ }}sharing{\text{ }}the{\text{ }}bond}}\]