Question

One of the refractive surfaces of a prism of angle ${{30}^{\circ }}$ is silvered. A ray incident at angle of ${{60}^{\circ }}$ retraces its paths. The refractive index of the material of prism is
$\text{A}\text{. }\sqrt{2}$
$\text{B}\text{. }\sqrt{3}$
$\text{C}\text{. }\dfrac{3}{2}$
$\text{A}\text{. 2}$

Answer 1

Hint: For the light ray to trace its path, it must hit the reflecting surface perpendicularly. Then with geometry, when the angle of refraction at the refracting surface. Then use Snell’s law and find the refractive index of the prism.

Formula used:
${{\mu }_{i}}\sin i={{\mu }_{r}}\sin r$

Complete answer:
It is given that one of the refractive surfaces of the prism is silvered. As a result, this surface for the prism will act as a mirror. It is given that the angle of the prism is ${{30}^{\circ }}$. Let the refractive index of the prism be $\mu $.
Then, it said that a ray of light is incident on the refracting surface (not silvered) at an angle of ${{60}^{\circ }}$. The ray will refract at this surface and fall on the silvered surface. Since, this surface is a mirror. the light will reflect at the surface.

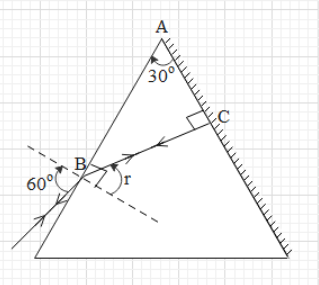
It is said that after reflecting at the second surface, the ray retraces its path. For this, the angle incidence for the reflecting surface must be zero. This means that the rays must hit the reflecting surface perpendicularly (as shown).
From Snell’s law, we get ${{\mu }_{i}}\sin i={{\mu }_{r}}\sin r$ ……. (i),
i and r the angles of incidence and refraction. ${{\mu }_{i}}$ and ${{\mu }_{r}}$ are the refractive indices of the mediums in which the ray is incident and refracted respectively.
In this case, i = ${{60}^{\circ }}$, ${{\mu }_{i}}$=1 and let ${{\mu }_{r}}$=$\mu $.
Consider the triangle ABC. In this triangle $\angle BAC=180-30-90={{60}^{\circ }}$.
As you can see in the figure, $\angle BAC=90-r$.
Therefore, we get that $60=90-r$.
$r=30$.
Substitute the values in equation (i).
$\Rightarrow 1\sin 60=\mu \sin 30$
$\Rightarrow \dfrac{\sqrt{3}}{2}=\mu \left( \dfrac{1}{2} \right)$
$\Rightarrow \mu =\sqrt{3}$.

Hence, the correct option is B.

Note:
Always remember the Snell’s equation properly. Many times students get confused in remembering the correct equation.
Remember that the refractive index of the medium in which the ray is incident and the angle of incidence come on the same side of the equation. Then you will know which quantities will come on the other side of the equation.