Question

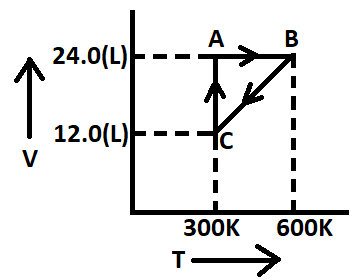
One mole of an ideal gas is put through a series of changes as shown in the graph in which A, B and C mark the three stages of the system. At each stage the variables are shown in the graph.
(a) Calculate the pressure at 3 stages of the system.
(b) Name the process during the following changes:
  (1) A to B
  (2) B to C
  (3) C to A
  (4) Overall change

Answer 1

Hint: (a)Given the values of volume, temperature and moles, we can calculate the value of pressure using the ideal gas equation.
(b)Also if volume during a process remains constant it is an isochoric, temperature remains constant it is isothermal, no heat change then it is adiabatic and pressure remains constant it is isobaric.

Formula used:
-Ideal gas equation: PV = nRT
Where, P = pressure
             V = volume
             n = moles
             R = gas constant = 0.082 L.atm.${K^{ - 1}}$.$mo{l^{ - 1}}$
             T = temperature


Complete step by step answer:
(a) The graph shows us the values of volume and temperature at every stage. So, to find out the value of pressure we will use the ideal gas equation:
                                                                 PV = nRT
The number of moles are given to be = 1 for all stages.
For stage (A): V = 24.0 L T = 300 K
       Now using equation (1): ${P_A} \times 24 = 1 \times 0.082 \times 300$
                                                       ${P_A} = \dfrac{{1 \times 0.082 \times 300}}{{24}}$
                                                             = 1.025 atm

For stage (B): The volume remains the same but temperature changes.
        V = 24.0 L T = 600 K
        Now using equation (1): ${P_A} \times 24 = 1 \times 0.082 \times 600$
                                                       ${P_A} = \dfrac{{1 \times 0.082 \times 600}}{{24}}$
                                                              = 2.05 atm

For stage (C): V = 12 L T = 300 K
Now using equation (1): ${P_A} \times 12 = 1 \times 0.082 \times 300$
                                                    ${P_A} = \dfrac{{1 \times 0.082 \times 300}}{{12}}$
                                                             = 2.05 atm

So, the pressure at stage (A) is 1.025 atm, at stage (B) is 2.05 atm and at stage (C) is 2.05 atm.
(b) Now we need to tell the process occurring during each transition and so we need to check which condition remains constant and which changes.
(1) A to B: During this change from A to B, we can see that volume remains constant at 24 L but temperature changes from 300 K to 600 K and pressure also changes from 1.025 to 2.05 atm.
So, this is an isochoric process.

(2) B to C: During this change we can see that volume decreases from 24 L to 12 L and temperature also decreases from 600 K to 300 K. But pressure remains constant at 2.05 atm.
So, this will be an isobaric process.

(3) C to A: During this change we can see that volume increases from 12 L to 24 L and pressure decreases from 2.05 to 1.025 atm. But the temperature remains constant at 300 K.
So, this is an isothermal process.

(4) Overall change: Overall we can see that the process starts from stage (A) and comes back to stage (A), so this is a cyclic process.

Note: (a)The value of R should be taken according to the units of temperature, pressure and volume.
      R = 8.314 $Pa.{m^3}.{K^{ - 1}}.mo{l^{ - 1}}$
      R = 0.08314 $bar.L.{K^{ - 1}}.mo{l^{ - 1}}$
      R= 8.314 $J.{K^{ - 1}}.mo{l^{ - 1}}$
      R= 0.082057 $L.atm.{K^{ - 1}}.mo{l^{ - 1}}$

(b) If temperature remains constant, then according to Boyle's law pressure and volume are inversely proportional to each other.
If pressure remains constant, then according to the Charles law volume is directly proportional to temperature.
If volume remains constant, then according to the Gay-Lussac’s Law temperature is directly proportional to pressure.