Question

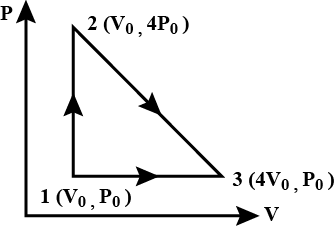
One mole of an ideal diatomic gas is taken through the cycle as shown in the figure:
 \[1 \to 2\]: isochoric process
 \[2 \to 3\]: a straight line of P-V diagram
 \[3 \to 1\]: isobaric process

The average molecular speed of the gas in the states 1, 2 and 3 in the ratio:

A. \[1:2:2\]
B. \[1:\sqrt 2 :\sqrt 2 \]
C. \[1:1:1\]
D. \[1:2:4\]

Answer 1

Hint: In \[1 \to 2\], Pressure is directly proportional to temperature. In \[3 \to 1\], Volume is directly proportional to Temperature. And the average molecular speed \[\left( {{V_{rms}}} \right)\] is directly proportional to $\sqrt {\dfrac{{RT}}{M}} $, hence \[v \propto \sqrt T \]​

Complete step by step answer:
In the state 1
Let temperature be \[{T_o}\]
and we know that, \[PV = nRT\]
In the state 2
Since \[1 \to 2\] is an isochoric process
Hence, in State 1
 $\dfrac{P}{T} = $ Constant
 \[v \propto {T_0}\] ​
when Pressure is equal to \[4{P_o}\]. Thus, the Temperature \[ = 4{T_o}\]​

State 3
Since \[3 \to 1\] is an isobaric process,
According to Charlee’s law
 \[V \propto T\]
 $\dfrac{V}{T} = $ Constant
When Volume is \[4{V_o}\]. Thus Temperature \[ = 4{T_o}\]

The root-mean-square speed or the average molecular speed \[\left( {{V_{rms}}} \right)\] is directly proportional to $\sqrt {\dfrac{{RT}}{M}} $
 \[ \Rightarrow v \propto \sqrt T \]​
The average velocity of the gas molecule has the formula : ​${V_{avg}} = \sqrt {\dfrac{{8RT}}{M}} $
Where,
V= molecular speed of the particle
T = Temperature in Kelvin
M = molar mass of the compound
R = Ideal gas constant

Hence,
 State 1, \[v \propto {T_0}\]​
 State 2, \[v \propto \sqrt {4{T_o}} = 2\sqrt {{T_o}} \]
 State3, \[v \propto \sqrt {4{T_o}} = 2\sqrt {{T_o}} \]
 Hence, \[{V_1}:{V_2}:{V_3} = \sqrt {{T_o}} :\sqrt {4{T_o}} :\sqrt {4Y{T_o}} \]
Ratio \[ = 1:2:2\]

Therefore, the correct answer is option (A).

Note: Isobaric process is carried out at a constant pressure. In such a process \[dP = 0\]. Isochoric process is a process in which the volume of the system remains constant, whereby \[dV = 0\]. According to the Kinetic Molecular Theory of Gases, the molecular speed of the gas explains that gas particles are in continuous motion and they exhibit ideally elastic collisions.