
One kind of cake required 200g flour and 25g of fat, and another kind of cake required 100g of flour and 50g of fat. Find the maximum number of cakes which can be made from 5kg of flour and 1kg of fat assuming that there is no shortage of other ingredients used in making the cakes?
Answer
604.8k+ views
Hint: We will form an equation according to the relation given like total flour = 5000g. So, the first equation will be \[200x+100y\le 5000\] and similarly, total fats available = 1000g, so, second equation will be $25x+50y\le 1000$ also the constraints \[x\ge 0,y\ge 0\] holds true. Then we will plot a graph and try to find the feasible region and then finally we will find the maximum number of cakes formed.
Complete step-by-step answer:
It is given in the question that one kind of cake requires 200g flour and 25g fat and another kind of cake requires 100g of flour and 500g of fat. Also Total flour available is 5kg and fat is 1Kg, then we have to find the maximum number of cakes which can be made. Let us assume that the number of the first type of cake will be x and Number of the second type of cake will be y. Thus, we get \[x\ge 0,y\ge 0\].
Now, we will put all the the given information in tabular form as following –
Let the total number of cake formed will be Z, then from table we get $Z=x+y$ and \[200x+100y\le 5000\] which is equal to $2x+y\le 50....(i)$ also, $25x+50y\le 1000$ which is equal to $x+2y\le 40.....(ii)$ and also \[x\ge 0,y\ge 0.....(iii)\]. Now, we will plot the graph according to the obtained equation.
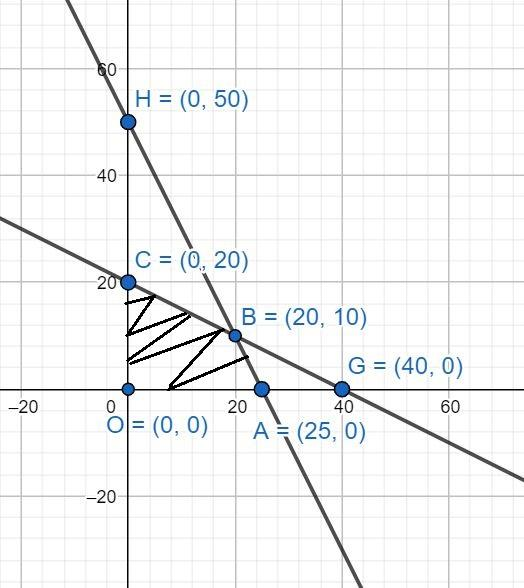
The corner points of feasible region ACBO are A(25,0), B(20,10), C(0,20) and O(0,0). Now, we can calculate the value of $Z=x+y$ by putting the value of corner points
Therefore, the maximum numbers of cakes that can be made are 30 assuming 20 of one kind and 10 of other kinds.
Note: Usually students do not plot graphs to solve linear inequality problems which create lots of problems for them many times. Also this results in the formation of wrong answers because without plotting graphs we can’t decide the feasible region and because of this many times students take wrong points or many times they may skip points. Thus, it is recommended to plot graphs in linear inequality questions.
Complete step-by-step answer:
It is given in the question that one kind of cake requires 200g flour and 25g fat and another kind of cake requires 100g of flour and 500g of fat. Also Total flour available is 5kg and fat is 1Kg, then we have to find the maximum number of cakes which can be made. Let us assume that the number of the first type of cake will be x and Number of the second type of cake will be y. Thus, we get \[x\ge 0,y\ge 0\].
Now, we will put all the the given information in tabular form as following –
| FLOUR(g) | FAT(g) | |
| Cakes of first kind(x) | 200 | 25 |
| Cakes of second kind(y) | 100 | 50 |
| Total available | 5000 | 1000 |
Let the total number of cake formed will be Z, then from table we get $Z=x+y$ and \[200x+100y\le 5000\] which is equal to $2x+y\le 50....(i)$ also, $25x+50y\le 1000$ which is equal to $x+2y\le 40.....(ii)$ and also \[x\ge 0,y\ge 0.....(iii)\]. Now, we will plot the graph according to the obtained equation.

The corner points of feasible region ACBO are A(25,0), B(20,10), C(0,20) and O(0,0). Now, we can calculate the value of $Z=x+y$ by putting the value of corner points
| Corner Point | $Z=x+y$ |
| A(25,0) | $Z=25+0=25$ |
| B(20,10) | $Z=20+10=30$ |
| C(0,20) | $Z=0+20=20$ |
| D(0,0) | $Z=0+0=0$ |
Therefore, the maximum numbers of cakes that can be made are 30 assuming 20 of one kind and 10 of other kinds.
Note: Usually students do not plot graphs to solve linear inequality problems which create lots of problems for them many times. Also this results in the formation of wrong answers because without plotting graphs we can’t decide the feasible region and because of this many times students take wrong points or many times they may skip points. Thus, it is recommended to plot graphs in linear inequality questions.
Recently Updated Pages
Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Trending doubts
What is the median of the first 10 natural numbers class 10 maths CBSE

Which women's tennis player has 24 Grand Slam singles titles?

Who is the Brand Ambassador of Incredible India?

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

A moving boat is observed from the top of a 150 m high class 10 maths CBSE




