Question

One end of a string of length $l$ is connected to a particle of mass $m$ and the other to a small peg on a smooth horizontal table. If the particle moves in a circle with speed $v$ the net force on the particle (directed towards the Centre) is:
A. $T$
B. $T - \dfrac{{m{v^2}}}{l}$
C. $T + \dfrac{{m{v^2}}}{l}$
D. 0

Answer 1

Hint: Draw free body diagram of the particle. Draw all forces acting in both vertical and horizontal directions on the particle. Cancel out the equal ones. And see the net resultant force acting on it.

Complete step by step answer:
It is given that; the particle is moving in a uniform circular motion (i.e. speed is constant) in a circle of radius \[l\]and speed\[v\].
The free body diagram of the particle will be:

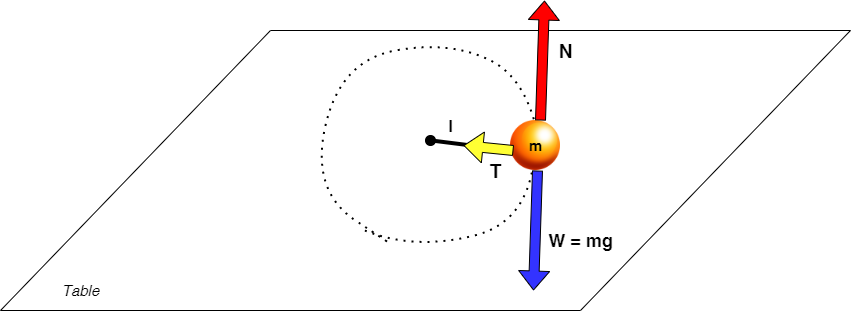
The particle experiences 3 types of forces:
force due to gravitational pull $mg$ (downwards),
normal reaction due to surface of table $N$ (upwards) and tension $T$ (radially inwards).
As we know that normal reaction $N$ and weight $mg$ are equal, they cancel out each other.
As we know, for an object to rotate uniformly in a circular motion there must be a centripetal force equal to $\dfrac{{m{v^2}}}{r}$ acting towards the center.
Here, the centripetal force $\dfrac{{m{v^2}}}{l}$ is provided by the tension in the string.
So, the net force acting on the body is equal to the tension i.e. $T$ .

So, the correct answer is “Option A”.

Note:
Take precautions while making the free body diagram of the particle. The student may get confused between the centripetal force and tension. It is to be remembered that centripetal force is simply the force that is necessary to keep an object moving in a circular path, and is directed inwards towards the center of rotation. Here this force required to keep the particle moving in its path is provided by the string, i.e. Tension. So, there is no need to draw centripetal force, again, separately in the free body diagram. That might give you incorrect answers.