Question

One diagonal of a square is the portion of the line $\sqrt 3 x + y = 2\sqrt 3 $ intercepted by the axes. Then an extremity of the other diagonal is.
$
  \left( a \right)\left( {1 + \sqrt 3 ,\sqrt 3 - 1} \right) \\
  \left( b \right)\left( {1 + \sqrt 3 ,\sqrt 3 + 1} \right) \\
  \left( c \right)\left( {1 - \sqrt 3 ,\sqrt 3 - 1} \right) \\
  \left( d \right)\left( {1 - \sqrt 3 ,\sqrt 3 + 1} \right) \\
$

Answer 1

Hint – In this question use the property that diagonal of the square bisect each other and are perpendicular to each other so the multiplication of slopes is equal to (-1) and the distance OA = OB = OC = OD so first find out the point O by using midpoint formula later on apply slope concept then apply the distance formula between two points ($x_1$, $y_1$) and ($x_2$, $y_2$) which is given as
$d = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} $ so use these concepts to reach the solution of the question.

Complete step-by-step answer:

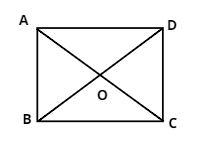
Let ABCD be the square as shown in figure,
AC and BD are the diagonals of the square.
The equation of one diagonal is $\sqrt 3 x + y = 2\sqrt 3 $ and it is also given that it intercepts the axis.
Let AC is the diagonal which is given.
Let point A on the y-axis and point B on the x-axis.
Therefore the coordinate on y-axis is (put x = 0), $\left( {0,2\sqrt 3 } \right)$
And the coordinate on x-axis is (put y = 0), $\left( {2,0} \right)$
Therefore the coordinates of A = $\left( {0,2\sqrt 3 } \right)$
And the coordinates of B = $\left( {2,0} \right)$.
Now as we know the diagonals of the square bisect each other and are perpendicular to each other.
Therefore OA = OB = OC = OD.
So O be the midpoint of diagonals AC and BD.
Now let, A = $\left( {0,2\sqrt 3 } \right)$ = ($x_1$, $y_1$) and B = $\left( {2,0} \right)$= ($x_2$, $y_2$).
So the coordinates of O according to midpoint formula is
$O = \left( {\dfrac{{{x_1} + {x_2}}}{2},\dfrac{{{y_1} + {y_2}}}{2}} \right) = \left( {\dfrac{{0 + 2}}{2},\dfrac{{2\sqrt 3 + 0}}{2}} \right) = \left( {1,\sqrt 3 } \right)$
Now the slope (m) of diagonal AC is m = $ - \sqrt 3 $ (as compared from y = mx + c, where m is the slope).
So diagonal AC and BD perpendicular to each other,
So the multiplication of slopes = -1
Let the slope of BD = $m_1$.
$ \Rightarrow m.{m_1} = - 1$
$ \Rightarrow {m_1} = \dfrac{{ - 1}}{m} = \dfrac{{ - 1}}{{ - \sqrt 3 }} = \dfrac{1}{{\sqrt 3 }}$
Now the equation of diagonal BD is
$y - {y_1} = {m_1}\left( {x - {x_1}} \right)$ (where, ($x_1$, $y_1$) is the point form which diagonal BD is passing).
So the diagonal BD is passing through O = $\left( {1,\sqrt 3 } \right)$.
$ \Rightarrow y - \sqrt 3 = \dfrac{1}{{\sqrt 3 }}\left( {x - 1} \right)$
$ \Rightarrow y\sqrt 3 - 3 = x - 1$.................... (1)
Now let coordinates of B = (p, q) and D = (r, s)
So these two coordinates satisfy the equation (1) therefore,
$ \Rightarrow q\sqrt 3 - 3 = p - 1$................... (2)
And
$ \Rightarrow s\sqrt 3 - 3 = r - 1$....................... (3)
Now the distance OA = OD................... (4)
As we know that the distance between two points ($x_1$, $y_1$) and ($x_2$, $y_2$) is given as
$d = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} $
Let A = $\left( {0,2\sqrt 3 } \right)$ = ($x_1$, $y_1$), O = $\left( {1,\sqrt 3 } \right)$ = ($x_2$, $y_2$) and D = (r, s) = ($x_3$, $y_3$)
Therefore $OA = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} = \sqrt {{{\left( {1 - 0} \right)}^2} + {{\left( {\sqrt 3 - 2\sqrt 3 } \right)}^2}} = \sqrt {1 + 3} = 2$
And $OD = \sqrt {{{\left( {{x_3} - {x_2}} \right)}^2} + {{\left( {{y_3} - {y_2}} \right)}^2}} = \sqrt {{{\left( {r - 1} \right)}^2} + {{\left( {s - \sqrt 3 } \right)}^2}} $
Therefore, from equation (4) we have,
$ \Rightarrow \sqrt {{{\left( {r - 1} \right)}^2} + {{\left( {s - \sqrt 3 } \right)}^2}} = 2$
$ \Rightarrow {\left( {r - 1} \right)^2} + {\left( {s - \sqrt 3 } \right)^2} = 4$
Now from equation (3) we have,
$ \Rightarrow {\left( {s\sqrt 3 - 3} \right)^2} + {\left( {s - \sqrt 3 } \right)^2} = 4$
Now expand the square we have,
$ \Rightarrow 3{s^2} + 9 - 6s\sqrt 3 + {s^2} + 3 - 2s\sqrt 3 = 4$
$ \Rightarrow 4{s^2} - 8s\sqrt 3 + 8 = 0$
$ \Rightarrow {s^2} - 2s\sqrt 3 + 2 = 0$
Now apply quadratic formula we have,
$ \Rightarrow s = \dfrac{{ - b \pm \sqrt {{b^2} - 4ac} }}{{2a}}$, where (a = 1, b = -2$\sqrt 3 $ and c = 2)
$ \Rightarrow s = \dfrac{{2\sqrt 3 \pm \sqrt {12 - 8} }}{2} = \dfrac{{2\sqrt 3 \pm 2}}{2} = \sqrt 3 \pm 1$
Now when s = $\sqrt 3 + 1$
From equation (3) we have,
$ \Rightarrow \left( {\sqrt 3 + 1} \right)\sqrt 3 - 3 = r - 1$
$ \Rightarrow 3 + \sqrt 3 - 3 = r - 1$
$ \Rightarrow r = \sqrt 3 + 1$
So the extremities of other diagonal is $\left( {r,s} \right) = \left( {\sqrt 3 + 1,\sqrt 3 + 1} \right)$
Now when s = $\sqrt 3 - 1$
From equation (3) we have,
$ \Rightarrow \left( {\sqrt 3 - 1} \right)\sqrt 3 - 3 = r - 1$
$ \Rightarrow 3 - \sqrt 3 - 3 = r - 1$
$ \Rightarrow r = - \sqrt 3 + 1$
So the extremities of other diagonal is $\left( {r,s} \right) = \left( {\sqrt 3 + 1,1 - \sqrt 3 } \right)$
So this is the required answer.
Hence option (B) is correct.

Note – Whenever we face such types of questions the key concept is the properties of square which is all stated above then using these properties first find out the intersection point of diagonals (as it is given that the given diagonal is intercepted by the axes so the coordinate of A by substituting x = 0 and the coordinate of C by substituting y = 0), then find out the slope of given diagonal then use the property of the multiplication of perpendicular lines slope is equal to (-1) so we calculate the slope of another diagonal then write the equation of this diagonal passing through point O and having slope ($m_1$) as above then use the concept that OA = OD, assume any coordinates for D which satisfies the equation of diagonal then calculate the distance OA and OD as above and equate them and solve these two equations as above we will get the required extremity of the other diagonal.