One angle of a triangle is ${{\left( \dfrac{2x}{3} \right)}^{g}}$ and another is ${{\left( \dfrac{3x}{2} \right)}^{\circ }}$, whilst the third angle is ${{\left( \dfrac{\pi x}{75} \right)}^{c}}$. Express them all in degrees.
Answer
Verified588.9k+ views
Hint: We will apply the concept of relationship between grade and radians. This is given by one right angle 90 degrees is equal to 100 grad. This can be numerically written as ${{90}^{\circ }}={{100}^{g}}$. Also, we will use the formula which is given by ${{\left( \pi \right)}^{c}}={{180}^{\circ }}$ to solve the question. This can also be written as ${{\left( 1 \right)}^{c}}={{\left( \dfrac{180}{\pi } \right)}^{\circ }}$ after dividing the equation by $\pi $.
Complete step-by-step answer:
According to the question we get the required diagram of the triangle which is shown below.
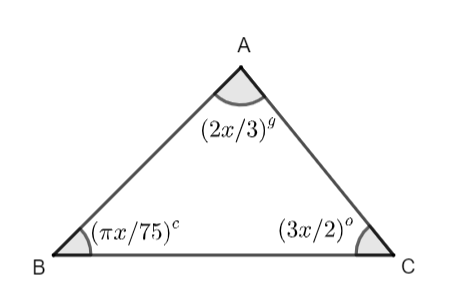
Now, we will consider the diagram for understanding the grade, radians and degree.
The grade is represented as the division of the degree into $\dfrac{10}{9}$ grades. The grade is represented as the division of 10 degrees into 9 grades. It is represented in the figure shown below.
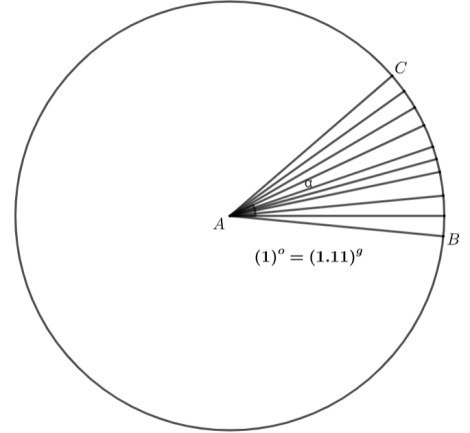
Here, ${{\left( 9 \right)}^{\circ }}$ is divided into ${{10}^{g}}$. The numerical formula is given by ${{90}^{\circ }}={{100}^{g}}$.
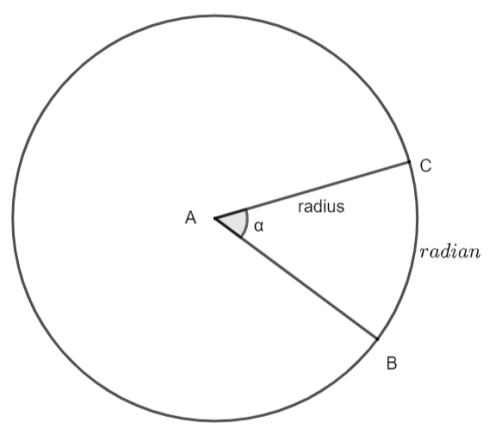
Also, the radian is an arc which is formed by two radiuses in a circle joining together at point A. Now, the relation between radians and degree is given by ${{\left( \pi \right)}^{c}}={{180}^{\circ }}$. This can also be written as ${{\left( 1 \right)}^{c}}={{\left( \dfrac{180}{\pi } \right)}^{\circ }}$ after dividing the equation by $\pi $. The diagram is shown below.
Now, we will consider ${{\left( \dfrac{2x}{3} \right)}^{g}}$ and we will convert into degrees by the formula given by ${{90}^{\circ }}={{100}^{g}}$ or, ${{\left( 1 \right)}^{g}}={{\left( \dfrac{9}{10} \right)}^{\circ }}$. We can write ${{\left( \dfrac{2x}{3} \right)}^{g}}$ as $\dfrac{2x}{3}\times {{\left( 1 \right)}^{g}}$. By substituting ${{\left( 1 \right)}^{g}}={{\left( \dfrac{9}{10} \right)}^{\circ }}$ in $\dfrac{2x}{3}\times {{\left( 1 \right)}^{g}}$ we get,
$\begin{align}
& \dfrac{2x}{3}\times {{\left( 1 \right)}^{g}}=\dfrac{2x}{3}\times {{\left( \dfrac{9}{10} \right)}^{\circ }} \\
& \Rightarrow \dfrac{2x}{3}\times {{\left( 1 \right)}^{g}}={{\left( \dfrac{2x}{3}\times \dfrac{9}{10} \right)}^{\circ }} \\
& \Rightarrow \dfrac{2x}{3}\times {{\left( 1 \right)}^{g}}={{\left( \dfrac{x}{1}\times \dfrac{3}{5} \right)}^{\circ }} \\
& \Rightarrow \dfrac{2x}{3}\times {{\left( 1 \right)}^{g}}={{\left( \dfrac{3x}{5} \right)}^{\circ }}...(i) \\
\end{align}$
Now we will consider ${{\left( \dfrac{3x}{2} \right)}^{\circ }}...(ii)$. Since, it is already in degrees so we will remain it as it is.
Now, we will consider ${{\left( \dfrac{\pi x}{75} \right)}^{c}}$ and we will convert the radians into degrees. As we know that ${{\left( \dfrac{\pi x}{75} \right)}^{c}}$ can be written as ${{\left( \dfrac{\pi x}{75} \right)}^{c}}=\dfrac{\pi x}{75}\times {{\left( 1 \right)}^{c}}$. Now, after this we will use the formula given by ${{\left( 1 \right)}^{c}}={{\left( \dfrac{180}{\pi } \right)}^{\circ }}$. Therefore, we have
$\begin{align}
& {{\left( \dfrac{\pi x}{75} \right)}^{c}}=\dfrac{\pi x}{75}\times {{\left( 1 \right)}^{c}} \\
& \Rightarrow {{\left( \dfrac{\pi x}{75} \right)}^{c}}=\dfrac{\pi x}{75}\times {{\left( \dfrac{180}{\pi } \right)}^{\circ }} \\
& \Rightarrow {{\left( \dfrac{\pi x}{75} \right)}^{c}}={{\left( \dfrac{\pi x}{75}\times \dfrac{180}{\pi } \right)}^{\circ }} \\
& \Rightarrow {{\left( \dfrac{\pi x}{75} \right)}^{c}}={{\left( \dfrac{x}{5}\times \dfrac{12}{1} \right)}^{\circ }} \\
& \Rightarrow {{\left( \dfrac{\pi x}{75} \right)}^{c}}={{\left( \dfrac{12x}{5} \right)}^{\circ }}...(iii) \\
\end{align}$
As we know that the sum of the angles of a triangle is equal to 180 degrees. Therefore, we have
$\begin{align}
& {{\left( \dfrac{2x}{3} \right)}^{g}}+{{\left( \dfrac{3x}{2} \right)}^{\circ }}+{{\left( \dfrac{\pi x}{75} \right)}^{c}}={{180}^{\circ }} \\
& \Rightarrow {{\left( \dfrac{3x}{5} \right)}^{\circ }}+{{\left( \dfrac{3x}{2} \right)}^{\circ }}+{{\left( \dfrac{12x}{5} \right)}^{\circ }}={{180}^{\circ }} \\
\end{align}$
Now as we know that the l.c.m. of 5, 2 and 5 is 10. Therefore, we have
$\begin{align}
& \Rightarrow {{\left( \dfrac{3x}{5}+\dfrac{3x}{2}+\dfrac{12x}{5} \right)}^{\circ }}={{180}^{\circ }} \\
& \Rightarrow {{\left( \dfrac{6x+15x+24x}{10} \right)}^{\circ }}={{180}^{\circ }} \\
& \Rightarrow {{\left( \dfrac{45x}{10} \right)}^{\circ }}={{180}^{\circ }} \\
& \Rightarrow \dfrac{45x}{10}=180 \\
& \Rightarrow x=180\times \dfrac{10}{45} \\
& \Rightarrow x=4\times \dfrac{10}{1} \\
& \Rightarrow x=40 \\
\end{align}$
Now, we will substitute the value of x in (i) thus we get ${{\left( \dfrac{3x}{5} \right)}^{\circ }}$ as ${{\left( \dfrac{3\left( 40 \right)}{5} \right)}^{\circ }}={{\left( \dfrac{120}{5} \right)}^{\circ }}$ or, ${{24}^{\circ }}$. After this we will substitute the value of x in (ii) therefore, we have
$\begin{align}
& {{\left( \dfrac{3x}{2} \right)}^{\circ }}={{\left( \dfrac{3\left( 40 \right)}{2} \right)}^{\circ }} \\
& \Rightarrow {{\left( \dfrac{3x}{2} \right)}^{\circ }}={{\left( \dfrac{120}{2} \right)}^{\circ }} \\
& \Rightarrow {{\left( \dfrac{3x}{2} \right)}^{\circ }}={{60}^{\circ }} \\
\end{align}$
And by substituting x = 40 in (iii) we have
$\begin{align}
& {{\left( \dfrac{12x}{5} \right)}^{\circ }}={{\left( \dfrac{12\left( 40 \right)}{5} \right)}^{\circ }} \\
& \Rightarrow {{\left( \dfrac{12x}{5} \right)}^{\circ }}={{\left( \dfrac{480}{5} \right)}^{\circ }} \\
& \Rightarrow {{\left( \dfrac{12x}{5} \right)}^{\circ }}={{96}^{\circ }} \\
\end{align}$
Hence, the required angles of a triangle are ${{24}^{\circ }},{{60}^{\circ }},{{96}^{\circ }}$.
Note: Always remember that the sum of all the interior angles of a triangle is equal to 180 degrees. Be aware to use $\pi ={{180}^{\circ }}$ and cancel the value. This will lead to wrong answers. First observe in what power the term is given to us which is going to be converted into degrees. As we can see that one angle is in grade, one in degrees and one is in radian. Then, apply the formula accordingly.
Complete step-by-step answer:
According to the question we get the required diagram of the triangle which is shown below.
Now, we will consider the diagram for understanding the grade, radians and degree.
The grade is represented as the division of the degree into $\dfrac{10}{9}$ grades. The grade is represented as the division of 10 degrees into 9 grades. It is represented in the figure shown below.
Here, ${{\left( 9 \right)}^{\circ }}$ is divided into ${{10}^{g}}$. The numerical formula is given by ${{90}^{\circ }}={{100}^{g}}$.
Also, the radian is an arc which is formed by two radiuses in a circle joining together at point A. Now, the relation between radians and degree is given by ${{\left( \pi \right)}^{c}}={{180}^{\circ }}$. This can also be written as ${{\left( 1 \right)}^{c}}={{\left( \dfrac{180}{\pi } \right)}^{\circ }}$ after dividing the equation by $\pi $. The diagram is shown below.
Now, we will consider ${{\left( \dfrac{2x}{3} \right)}^{g}}$ and we will convert into degrees by the formula given by ${{90}^{\circ }}={{100}^{g}}$ or, ${{\left( 1 \right)}^{g}}={{\left( \dfrac{9}{10} \right)}^{\circ }}$. We can write ${{\left( \dfrac{2x}{3} \right)}^{g}}$ as $\dfrac{2x}{3}\times {{\left( 1 \right)}^{g}}$. By substituting ${{\left( 1 \right)}^{g}}={{\left( \dfrac{9}{10} \right)}^{\circ }}$ in $\dfrac{2x}{3}\times {{\left( 1 \right)}^{g}}$ we get,
$\begin{align}
& \dfrac{2x}{3}\times {{\left( 1 \right)}^{g}}=\dfrac{2x}{3}\times {{\left( \dfrac{9}{10} \right)}^{\circ }} \\
& \Rightarrow \dfrac{2x}{3}\times {{\left( 1 \right)}^{g}}={{\left( \dfrac{2x}{3}\times \dfrac{9}{10} \right)}^{\circ }} \\
& \Rightarrow \dfrac{2x}{3}\times {{\left( 1 \right)}^{g}}={{\left( \dfrac{x}{1}\times \dfrac{3}{5} \right)}^{\circ }} \\
& \Rightarrow \dfrac{2x}{3}\times {{\left( 1 \right)}^{g}}={{\left( \dfrac{3x}{5} \right)}^{\circ }}...(i) \\
\end{align}$
Now we will consider ${{\left( \dfrac{3x}{2} \right)}^{\circ }}...(ii)$. Since, it is already in degrees so we will remain it as it is.
Now, we will consider ${{\left( \dfrac{\pi x}{75} \right)}^{c}}$ and we will convert the radians into degrees. As we know that ${{\left( \dfrac{\pi x}{75} \right)}^{c}}$ can be written as ${{\left( \dfrac{\pi x}{75} \right)}^{c}}=\dfrac{\pi x}{75}\times {{\left( 1 \right)}^{c}}$. Now, after this we will use the formula given by ${{\left( 1 \right)}^{c}}={{\left( \dfrac{180}{\pi } \right)}^{\circ }}$. Therefore, we have
$\begin{align}
& {{\left( \dfrac{\pi x}{75} \right)}^{c}}=\dfrac{\pi x}{75}\times {{\left( 1 \right)}^{c}} \\
& \Rightarrow {{\left( \dfrac{\pi x}{75} \right)}^{c}}=\dfrac{\pi x}{75}\times {{\left( \dfrac{180}{\pi } \right)}^{\circ }} \\
& \Rightarrow {{\left( \dfrac{\pi x}{75} \right)}^{c}}={{\left( \dfrac{\pi x}{75}\times \dfrac{180}{\pi } \right)}^{\circ }} \\
& \Rightarrow {{\left( \dfrac{\pi x}{75} \right)}^{c}}={{\left( \dfrac{x}{5}\times \dfrac{12}{1} \right)}^{\circ }} \\
& \Rightarrow {{\left( \dfrac{\pi x}{75} \right)}^{c}}={{\left( \dfrac{12x}{5} \right)}^{\circ }}...(iii) \\
\end{align}$
As we know that the sum of the angles of a triangle is equal to 180 degrees. Therefore, we have
$\begin{align}
& {{\left( \dfrac{2x}{3} \right)}^{g}}+{{\left( \dfrac{3x}{2} \right)}^{\circ }}+{{\left( \dfrac{\pi x}{75} \right)}^{c}}={{180}^{\circ }} \\
& \Rightarrow {{\left( \dfrac{3x}{5} \right)}^{\circ }}+{{\left( \dfrac{3x}{2} \right)}^{\circ }}+{{\left( \dfrac{12x}{5} \right)}^{\circ }}={{180}^{\circ }} \\
\end{align}$
Now as we know that the l.c.m. of 5, 2 and 5 is 10. Therefore, we have
$\begin{align}
& \Rightarrow {{\left( \dfrac{3x}{5}+\dfrac{3x}{2}+\dfrac{12x}{5} \right)}^{\circ }}={{180}^{\circ }} \\
& \Rightarrow {{\left( \dfrac{6x+15x+24x}{10} \right)}^{\circ }}={{180}^{\circ }} \\
& \Rightarrow {{\left( \dfrac{45x}{10} \right)}^{\circ }}={{180}^{\circ }} \\
& \Rightarrow \dfrac{45x}{10}=180 \\
& \Rightarrow x=180\times \dfrac{10}{45} \\
& \Rightarrow x=4\times \dfrac{10}{1} \\
& \Rightarrow x=40 \\
\end{align}$
Now, we will substitute the value of x in (i) thus we get ${{\left( \dfrac{3x}{5} \right)}^{\circ }}$ as ${{\left( \dfrac{3\left( 40 \right)}{5} \right)}^{\circ }}={{\left( \dfrac{120}{5} \right)}^{\circ }}$ or, ${{24}^{\circ }}$. After this we will substitute the value of x in (ii) therefore, we have
$\begin{align}
& {{\left( \dfrac{3x}{2} \right)}^{\circ }}={{\left( \dfrac{3\left( 40 \right)}{2} \right)}^{\circ }} \\
& \Rightarrow {{\left( \dfrac{3x}{2} \right)}^{\circ }}={{\left( \dfrac{120}{2} \right)}^{\circ }} \\
& \Rightarrow {{\left( \dfrac{3x}{2} \right)}^{\circ }}={{60}^{\circ }} \\
\end{align}$
And by substituting x = 40 in (iii) we have
$\begin{align}
& {{\left( \dfrac{12x}{5} \right)}^{\circ }}={{\left( \dfrac{12\left( 40 \right)}{5} \right)}^{\circ }} \\
& \Rightarrow {{\left( \dfrac{12x}{5} \right)}^{\circ }}={{\left( \dfrac{480}{5} \right)}^{\circ }} \\
& \Rightarrow {{\left( \dfrac{12x}{5} \right)}^{\circ }}={{96}^{\circ }} \\
\end{align}$
Hence, the required angles of a triangle are ${{24}^{\circ }},{{60}^{\circ }},{{96}^{\circ }}$.
Note: Always remember that the sum of all the interior angles of a triangle is equal to 180 degrees. Be aware to use $\pi ={{180}^{\circ }}$ and cancel the value. This will lead to wrong answers. First observe in what power the term is given to us which is going to be converted into degrees. As we can see that one angle is in grade, one in degrees and one is in radian. Then, apply the formula accordingly.
Recently Updated Pages
Master Class 11 Social Science: Engaging Questions & Answers for Success
Master Class 11 Physics: Engaging Questions & Answers for Success
Master Class 11 Maths: Engaging Questions & Answers for Success
Master Class 11 Economics: Engaging Questions & Answers for Success
Master Class 11 Computer Science: Engaging Questions & Answers for Success
Master Class 11 Chemistry: Engaging Questions & Answers for Success
Trending doubts
What is meant by exothermic and endothermic reactions class 11 chemistry CBSE
10 examples of friction in our daily life
Difference Between Prokaryotic Cells and Eukaryotic Cells
1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE
Draw a diagram of nephron and explain its structur class 11 biology CBSE