Question

On which law, Kepler’s second law is based?
${\text{A}}{\text{.}}$ Newton’s first law
${\text{B}}{\text{.}}$ Newton’s second law
${\text{C}}{\text{.}}$ Special theory of relativity
${\text{D}}{\text{.}}$ Conservation of angular momentum

Answer 1

Hint: Here, we will proceed by stating the Kepler’s second law of planetary motion. Then, we will consider a wedge (basically an arc) and assume it to be a triangle. Finally, we will apply Kepler’s second law in it.
Formulas Used- Length of the arc = r$\theta $, Area of triangle = $\dfrac{1}{2}$(Base of triangle)(Height of the triangle), $\omega $ = $\dfrac{{d\theta }}{{dt}}$ and L = $m\omega {r^2}$.

Complete Step-by-Step solution:
Statement of Kepler's second law of planetary motion is that if an imaginary line is drawn from the centre of the sun to the centre of any planet, then equal amounts of areas will be swept in equal time intervals. This law is also known as the law of equal areas. This means that the derivative of an area with respect to time is always constant.
i.e., $\dfrac{{d{\text{A}}}}{{dt}}$ = constant $ \to (1)$
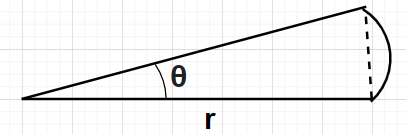
Let us consider a wedge swept by this imaginary line in a small time interval dt as shown in figure. Let r be the distance between the centre of the sun and that of the planet. Also, let us assume that the angle made at the centre of the sun by this wedge in dt time interval be $d\theta $. The angular velocity of the planet is $\omega $ (say).
As we know that the length of an arc of radius r and subtending an angle of $\theta $ at the centre is given by
Length of the arc = r$\theta $
Using the above formula, we can write
Length of the wedge arc = r$d\theta $
Since, this wedge is so small (as $d\theta $ is very small) that it can be assumed to be triangular in shape. Also, we know that the area of any triangle is given by
Area of triangle = $\dfrac{1}{2}$(Base of triangle)(Height of the triangle)
Using the above formula, we can write
Area of the wedge dA = $\dfrac{1}{2}$(Radius of the arc)(Length of the wedge arc)
Area of the wedge dA = $\dfrac{1}{2}$(r)(r$d\theta $) = $\dfrac{1}{2}{r^2}d\theta $
By dividing the above equation with dt on both sides, we get
$
  \dfrac{{d{\text{A}}}}{{dt}} = \dfrac{{\left( {\dfrac{1}{2}{r^2}d\theta } \right)}}{{dt}} \\
   \Rightarrow \dfrac{{d{\text{A}}}}{{dt}} = \dfrac{1}{2}\left( {\dfrac{{{r^2}d\theta }}{{dt}}} \right) \\
   \Rightarrow \dfrac{{d{\text{A}}}}{{dt}} = \dfrac{{{r^2}}}{2}\left( {\dfrac{{d\theta }}{{dt}}} \right){\text{ }} \to {\text{(2)}} \\
 $
As we know that the rate of change of the angular position is termed as angular velocity denoted by $\omega $ i.e., $\omega $ = $\dfrac{{d\theta }}{{dt}}{\text{ }} \to {\text{(3)}}$
Using equation (3) in equation (2), we have
$
   \Rightarrow \dfrac{{d{\text{A}}}}{{dt}} = \dfrac{{{r^2}}}{2}\left( \omega \right) \\
   \Rightarrow \dfrac{{d{\text{A}}}}{{dt}} = \dfrac{{\omega {r^2}}}{2}{\text{ }} \to {\text{(4)}} \\
 $
Also, angular momentum of the body having mass m, angular velocity $\omega $ and radius r is given by
L = $m\omega {r^2}$
$ \Rightarrow \omega {r^2} = \dfrac{{\text{L}}}{m}$
By using $\omega {r^2} = \dfrac{{\text{L}}}{m}$ in equation (4), we get
$ \Rightarrow \dfrac{{d{\text{A}}}}{{dt}} = \dfrac{{\left( {\dfrac{{\text{L}}}{m}} \right)}}{2} = \dfrac{{\text{L}}}{{2m}}$
According to Kepler’s second law (or equation (1)), we can write
$\dfrac{{\text{L}}}{{2m}}$ = constant
$ \Rightarrow $ L = constant as mass of the planet will be fixed and will not vary
So, the angular momentum remains constant which simply refers to the law of conservation of angular momentum.

Therefore, option D is correct.

Note- Newton’s first law of motion states that the body which is in a state of rest or in uniform motion will remain to be in that state unless an external force is applied to it. Newton’s second law of motion states that the resultant external force acting on the body is equal to the product of mass and acceleration of the body.