Question

On the same side of a tower, two objects are located. When observed from the top of the tower, their angles of depression are \[{{45}^{\circ }}\]and \[{{60}^{\circ }}\]. If the height of the tower is 150 m, fine the distance between the objects.

Answer 1

Hint: consider the maximum height as AB and draw the angle of depression at two different points and apply \[\tan \theta \]to the two right angled triangles and we will get two equations and then we have to compute the maximum height from which he falls.

Complete step-by-step answer:

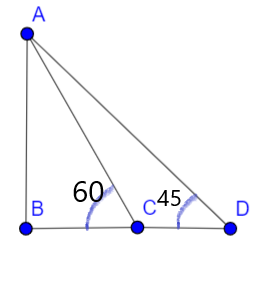
Given that the height of the tower is 150 m.

Let the two objects be placed at point C and D respectively.

In \[\Delta ABC\]

\[\tan {{60}^{\circ }}=\dfrac{150}{BC}\]

\[BC=\dfrac{150}{\sqrt{3}}\]

BC \[=86.7m\]. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . (1)

Now in \[\Delta ABD\]

\[\tan {{45}^{\circ }}=\dfrac{150}{BD}\]

\[BD=150m\]. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . (2)

From (1) and (2)

Now the distance between the objects is \[CD=BD-BC\]

\[=150-86.7\]

\[=63.3m\]

Note: If the object observed by the observer is below the level of the observer, then the angle formed between the horizontal line and the observer’s line of sight is called the angle of depression. As the person moves from one point to another angle of depression varies.