Question

On the same graph paper. Plot the graph of $y = 2x - 1,{\text{ }}y = 2x$ and $y = 2x + 1$ from $x = - 2$ to $x = 4$
The graphs (lines) drawn are
A) Intersecting but not at right angles
B) Forming a square
C) Parallel to each other
D) Forming a triangle and a segment.

Answer 1

Hint: First, we have given the three straight line equations. And students asked to plot the graph by substituting some negative value of $x$ to some positive value of $x$. Then we have found how the lines in the same graphs are acting like they intersect or forming some shapes or they are parallel.

Complete step-by-step answer:
Given straight line equations are
$\left( i \right){\text{ }}y = 2x - 1$
$\left( {ii} \right){\text{ }}y = 2x$ and
$\left( {iii} \right){\text{ }}y = 2x + 1$
We have to plot the graph of these straight lines from $x = - 2$ to $x = 4$. That is $x = - 2, - 1,0,1,2,3,4$
Let us take the first equation $y = 2x - 1$
If $x = - 2$ we get $y = - 5$
If $x = - 1$ we get $y = - 3$
If $x = 0$ we get $y = - 1$
If $x = 1$ we get $y = 1$
If $x = 2$ we get $y = 3$
If $x = 3$ we get $y = 5$
If $x = 4$ we get $y = 7$
$\therefore $The points for $y = 2x - 1$ from $x = - 2{\text{ to }}x = 4$ are $\left( { - 2, - 5} \right),\left( { - 1, - 3} \right),\left( {0, - 1} \right),\left( {1,1} \right),\left( {2,3} \right),\left( {3,5} \right),\left( {4,7} \right)$
Let us take the first equation $y = 2x$
If $x = - 2$ we get $y = - 4$
If $x = - 1$ we get $y = - 2$
If $x = 0$ we get $y = 0$
If $x = 0$ we get $y = 0$
If $x = 1$ we get $y = 2$
If $x = 2$we get $y = 4$
If $x = 3$ we get $y = 6$
If $x = 4$ we get $y = 8$
$\therefore $The points for $y = 2x$ from $x = - 2{\text{ to }}x = 4$ are $\left( { - 2, - 4} \right),\left( { - 1, - 2} \right),\left( {0,0} \right),\left( {1,2} \right),\left( {2,4} \right),\left( {3,6} \right),\left( {4,8} \right)$
Let us take the first equation $y = 2x + 1$
If $x = - 2$ we get $y = - 3$
If $x = - 1$ we get $y = - 1$
If $x = 0$ we get $y = 1$
If $x = 1$ we get $y = 3$
If $x = 2$we get $y = 5$
If $x = 3$ we get $y = 7$
If $x = 4$ we get $y = 9$
$\therefore $ The points for $y = 2x + 1$ from $x = - 2{\text{ to }}x = 4$ are $\left( { - 2, - 3} \right),\left( { - 1, - 1} \right),\left( {0,1} \right),\left( {1,3} \right),\left( {2,5} \right),\left( {3,7} \right),\left( {4,9} \right)$
Now we are going to substitute the points in the graph. We get,

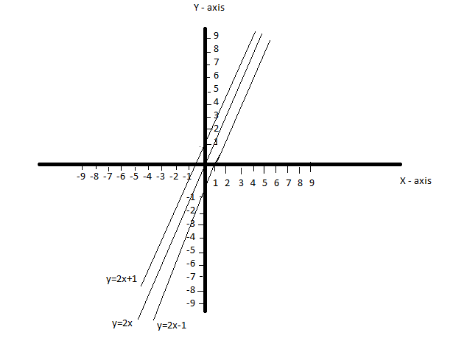
As shown in the above graph (lines) drawn are parallel to each other.

Option C is the correct answer.

Note: Students need to be careful while substituting the points in the given straight lines. Parallel lines are in a plane do not intersect at any point and keep a fixed minimum distance and parallel lines may be horizontal, vertical or slanted.