Question

On the parabola $y={{x}^{2}}$ , the point least distant from the straight line $y=2x-4$ is.
(a) $\left( 1,1 \right)$
(b) $\left( 1,0 \right)$
(c) $\left( 1,-1 \right)$
(d) $\left( 0,0 \right)$

Answer 1

Hint: For solving this question first we will consider a point $\left( t,{{t}^{2}} \right)$ on the parabola $y={{x}^{2}}$ and find the perpendicular distance of the point $\left( t,{{t}^{2}} \right)$ from the line $y=2x-4$ with the help of the formula $\dfrac{\left| a{{x}_{1}}+b{{y}_{1}}+c \right|}{\sqrt{{{a}^{2}}+{{b}^{2}}}}$ . After that, we will analyse the expression of the perpendicular distance and try to find the value of $t$ for which the perpendicular distance is minimum and answer the question correctly.

Complete step-by-step solution -
Given:
We have a parabola $y={{x}^{2}}$ and we have to find a point on the parabola which is at least possible distance from the line $y=2x-4$ .
Now, before we proceed we should know the following important concepts of the coordinate geometry:
1. For a parabola of the form, ${{x}^{2}}=y$ the parametric coordinates of any point on it can take as $\left( t,{{t}^{2}} \right)$ where $t$ is a variable parameter.
2. If a point $A\equiv \left( {{x}_{1}},{{y}_{1}} \right)$ is not on the line $ax+by+c=0$ then the length of the perpendicular from point A on the line $ax+by+c=0$ will be equal to the value of $\dfrac{\left| a{{x}_{1}}+b{{y}_{1}}+c \right|}{\sqrt{{{a}^{2}}+{{b}^{2}}}}$ .
3. If the minimum value of $f\left( x \right)$ occurs at $x={{x}_{1}}$ then, ${f}'\left( {{x}_{1}} \right)={{\left[ \dfrac{d\left( f\left( x \right) \right)}{dx} \right]}_{x={{x}_{1}}}}=0$ and ${f}''\left( {{x}_{1}} \right)={{\left[ \dfrac{d\left( {f}'\left( x \right) \right)}{dx} \right]}_{x={{x}_{1}}}}>0$ .
Now, we will use the above three concepts for solving this question.
Now, let there is a point $A\equiv \left( t,{{t}^{2}} \right)$ on the parabola $y={{x}^{2}}$ which is at least distance from the line $y=2x-4$ or $y+4-2x=0$ and $L$ is the length of the perpendicular from the point $A\equiv \left( t,{{t}^{2}} \right)$ on the line $2x-y-4=0$ so, using the second concept from the above-mentioned concepts. Then,
$\begin{align}
  & L=\dfrac{\left| {{t}^{2}}+4-2t \right|}{\sqrt{{{2}^{2}}+{{1}^{2}}}} \\
 & \Rightarrow L=\dfrac{\left| {{t}^{2}}+{{1}^{2}}-2t+3 \right|}{\sqrt{4+1}} \\
 & \Rightarrow L=\dfrac{\left| {{t}^{2}}+{{1}^{2}}-2t+3 \right|}{\sqrt{5}} \\
\end{align}$
Now, we can write ${{t}^{2}}+{{1}^{2}}-2t={{\left( t-1 \right)}^{2}}$ . Then,
$\begin{align}
  & L=\dfrac{\left| {{t}^{2}}+{{1}^{2}}-2t+3 \right|}{\sqrt{5}} \\
 & \Rightarrow L=\dfrac{\left| {{\left( t-1 \right)}^{2}}+3 \right|}{\sqrt{5}} \\
\end{align}$
Now, as the value of ${{\left( t-1 \right)}^{2}}+3$ will be always positive so, $\left| {{\left( t-1 \right)}^{2}}+3 \right|={{\left( t-1 \right)}^{2}}+3$ . Then,
$\begin{align}
  & L=\dfrac{\left| {{\left( t-1 \right)}^{2}}+3 \right|}{\sqrt{5}} \\
 & \Rightarrow L=\dfrac{{{\left( t-1 \right)}^{2}}+3}{\sqrt{5}} \\
\end{align}$
Now, we have to find the value of $t$ for which value of $L=\dfrac{{{\left( t-1 \right)}^{2}}+3}{\sqrt{5}}$ will be minimum for which value of ${{\left( t-1 \right)}^{2}}$ has to be minimum. And we know that ${{\left( t-1 \right)}^{2}}$ will be always positive and minimum value of ${{\left( t-1 \right)}^{2}}$ will be 0. Then,
$\begin{align}
  & {{\left( t-1 \right)}^{2}}=0 \\
 & \Rightarrow t-1=0 \\
 & \Rightarrow t=1 \\
\end{align}$
Now, from the above result, we conclude that for $t=1$ the value of ${{\left( t-1 \right)}^{2}}$ will be minimum and so, the value of $L=\dfrac{{{\left( t-1 \right)}^{2}}+3}{\sqrt{5}}$ will be minimum. And the minimum value of $L=\dfrac{3}{\sqrt{5}}$ .
Now, coordinates of the point A will be $A\equiv \left( 1,1 \right)$ . For more clarity look at the figure given below:

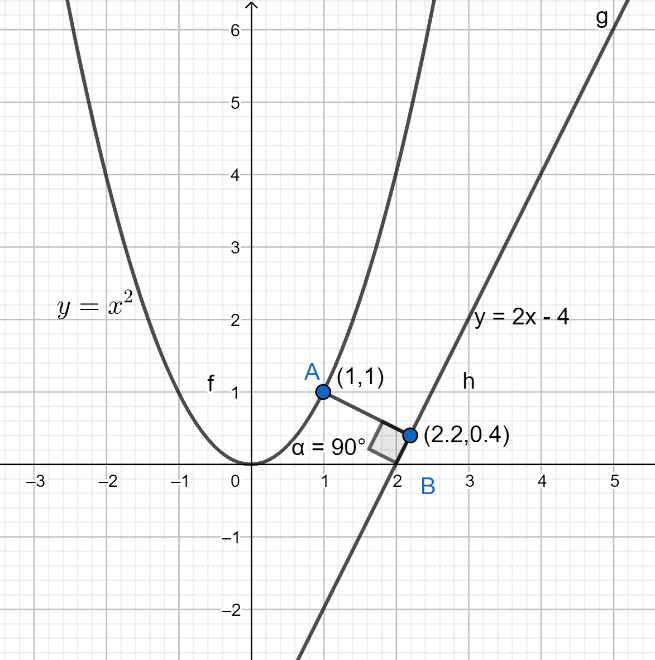
Hence, (a) is the correct option.

Note: Here, the student should first understand what is asked in the question and then proceed in the right direction to get the correct answer quickly. After that, we should substitute values in the formula without any mistake. Moreover, we can solve it by using options as points in the option (a) and (b) lie on the parabola and when we plot the given curves then, point (1,1) will be at the shortest possible distance.