Question

On a straight line passing through the foot of the tower, two points C and D are at distances of 4 m and 16 m from the foot respectively. If the angles of elevation from C and D of the top of the tower are complementary, then find the height of the tower.

Answer 1

Hint: Use the formula for tangent of an angle,
\[\tan \theta =\dfrac{Opposite\,side}{Adjacent\,side}\]
Use properties of complementary angles. Complementary angles are angles that sum up to \[{{90}^{\circ }}\]. Let, A and B be two angles, they are said to be complementary angles of each other if$A+B={{90}^{\circ }}$.
Use the trigonometric formula, \[\cot \theta =\dfrac{1}{\tan \theta }\]
Draw diagrams for ease of understanding the question.

Complete step by step answer:
We are given, two points C and D are at distances of 4 m and 16 m from the foot respectively. We are also given that the angles of elevation from C and D of the top of the tower are complementary.
We are asked to find the height of the tower.
Taking AB to be the tower mentioned in the question (with a height $h$ ),
We can represent the scenario as,

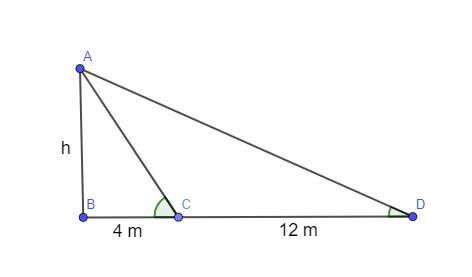
Here, \[\angle C\]and \[\angle D\] are complementary angles.
Hence,
\[\angle C={{90}^{\circ }}-\angle D\ and\,\angle D={{90}^{\circ }}-\angle C\]
From\[\Delta ABC\],
We know that \[\tan \theta =\dfrac{Opposite\,side}{Adjacent\,side}\]
\[\therefore \tan C=\dfrac{h}{4}\,...............(1)\]
From \[\Delta ABD\],
We know that \[\tan \theta =\dfrac{Opposite\,side}{Adjacent\,side}\]
\[\tan D=\tan ({{90}^{\circ }}-C)=\dfrac{h}{12+4}\]
\[\cot C=\dfrac{h}{16}..............(2)\]
We know the trigonometric equation,
\[\cot \theta =\dfrac{1}{\tan \theta }\]
Hence, using this trigonometric equation, equation (2) becomes,
\[\tan C=\dfrac{16}{h}..............(3)\]
On equating equation (1) and (2), we obtain,
\[\begin{align}
  & \dfrac{16}{h}=\dfrac{h}{4} \\
 & \\
\end{align}\]
On cross-multiplying,
\[\begin{align}
  & {{h}^{2}}=64 \\
 & \\
\end{align}\]
On taking square root of both the side,
\[h=\pm 8\]
Since, measurement of lengths cannot be a negative value, we reject the value of \[h=-8\].
\[\therefore h=8m\]
Hence, the height of the tower is 8m.

Note:
The same question could have been asked keeping the distance of points from the foot of the perpendicular as unknowns and to find those distances (Height would be given in this case). Nevertheless, the method would remain the same.
You have to keep in mind the difference between angle of elevation and angle of depression. Do not confuse it with each other.