Question

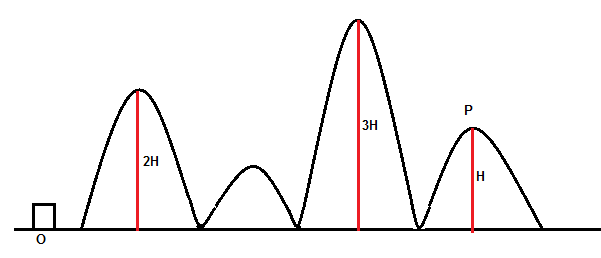
On a smooth curved track shown in the diagram, a small particle is projected from the point O, and that it just manages to reach the point P. Assume that particles always remain in contact with the track. The velocity of the particle on reaching the point P will be equal to:
(A) $ zero $
(B) $ \sqrt {2gH} $
(C) $ \sqrt {6gH} $
(D) $ \sqrt {4gH} $

Answer 1

Hint :O is the given particle as shown in the figure, it moves along the described trajectory and it is in contact with the track. We have to find out the velocity of particle O to reach the particle at the position named as P in the figure. Here we have the height of the particle at a different position and P is at the height $ H $ . Let us use the concept of kinetic energy to be used here.

Complete Step By Step Answer:
Here, the particle should have the initial velocity such that the particle should reach the maximum height $ 3H $ and velocity $ v = 0 $ at the highest point.
Now, here it is known that the point P is at the height of $ H $ and we have to consider the velocity at point P as $ {v_p} $ .
From this information we can be able to find out the work done by the gravity from highest point to Point P, such that $ {W_g} $ is given by
 $ {W_g} = 2mg(3H - H) $
 $ \Rightarrow {W_g} = 2mgH $
Since, here on particle O the gravity is acting so we have to use the work energy theorem to find out the velocity of O at point P.
Applying, work energy theorem, we get
 $ \Delta K.E. = {W_g} $
 $ \Rightarrow \dfrac{m}{2}(v_p^2 - {0^2}) = 2mgH $ (here, we have to use initial and final velocities of the particle)
 $ \Rightarrow v_p^2 = 4gH $
 $ \Rightarrow {v_p} = \sqrt {4gH} $
Hence, velocity of particle at point P is $ \sqrt {4gH} $ .
Thus, the correct option is D.

Note :
We have used the concept of work energy theorem as we observed that the work done here is under the influence of gravity and we have initial and final velocities of the particle. The formula we used here was: $ \Delta K.E. = {W_g} \Rightarrow \dfrac{m}{2}(velocity_{final}^2 - velocity_{initial}^2) = {W_g} $ .