Question

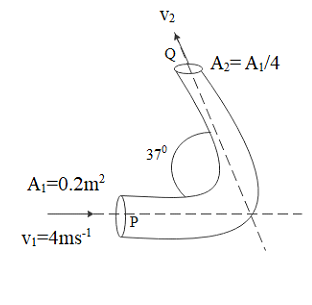
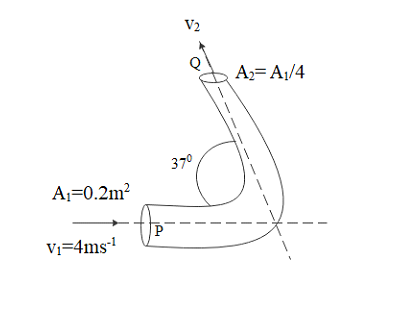
Oil enters the bend of a pipe in the horizontal plane with velocity $4m{s^{ - 1}}$ and pressure $280 \times {10^3}N{m^{ - 2}}$ as shown in the figure, the pressure of oil at the point Q in ($kN{m^{ - 2}}$) is (Take specific gravity of oil as 0.9 and $\sin {37^0} = 0.6$).

Answer 1

Hint: Bernoulli’s equation is the base for fluid mechanics and it is used to manufacture several machines. Machines like pump and diffuser are vastly used in the mechanical industry in order to extract the desired characteristics from the fluid flowing through them. By using bernoulli’s theorem we can solve this.

Formula used:
$\eqalign{
  & {A_1}{v_1} = {A_2}{v_2} \cr
  & {P_1} + 0.5\rho {v_1}^2 = {P_2} + 0.5\rho {v_2}^2 \cr} $

Complete step by step answer:
It is clearly mentioned that the pipe is in a horizontal plane which means there is no effect of height variation in pressure change. As fluid is flowing through the pipe its density doesn’t vary. So we can apply the equation of continuity over here. This states that for an incompressible fluid the product of area of cross section and velocity at any point will be the same.
 

That means
${A_1}{v_1} = {A_2}{v_2}$
By substituting the values from above diagram we will get
${A_1}{v_1} = {A_2}{v_2}$
$\eqalign{
   0.2 \times 4 = 0.05 \times {v_2} \cr
   {v_2} = 16 \cr} $
We have got the velocity at the required point. Now by applying bernoulli’s theorem we can find out the pressure at the point required.
Bernoulli’s theorem states that
${P_1} + 0.5\rho {v_1}^2 = {P_2} + 0.5\rho {v_2}^2$
By substituting the values given, we will get
Pressure at point 1 is 280 kilo pascal and the velocity of fluid at point 1 is 4 meter per second and the velocity of fluid at point 2 is 16 meter per second and the specific gravity of oil is 0.9
$\Rightarrow 280 \times {10^3} + 0.5\left( {900} \right){4^2} = {P_2} + 0.5\left( {900} \right){16^2} $
$\Rightarrow {P_2} = 280000 - 108000 $
$\Rightarrow {P_2} = 172000 pascal $
$\Rightarrow {P_2} = 172 kilopascal $
$\therefore {P_2} = 172 Kpa $

So the pressure at the exit of the pipe will be 172 kilo pascal.

Note:
In the question, we were given with specific gravity but we can’t directly substitute it in the equation. Specific gravity is the ratio of density of oil to the density of water as we take water as the reference liquid. So specific gravity must be multiplied with the density of water to use that in calculations.