Question

Of the number of three athletic teams in a school, 21 are in the basketball team, 26 in hockey team, 29 in the football team. 14 play hockey and basketball, 15 play hockey and football, 12 play football and basketball and 8 play all the games. The total number of members is
A) 42
B) 43
C) 45
D) None of these

Answer 1

Hint:
Here, we will use the concept of applications on the cardinality of the set. A set is defined as the collection of well defined objects. Cardinality of a set is defined as the number of elements in a set. We will substitute the given values in the formula of union of sets and simplify it to get the total number of members.

Formula Used:
If we are given three finite set, then the total number is given by the formula \[n\left( {A \cup B \cup C} \right) = n\left( A \right) + n\left( B \right) + n\left( C \right) - n\left( {A \cap B} \right) - n\left( {B \cap C} \right) - n\left( {A \cap C} \right) + n\left( {A \cap B \cap C} \right)\]

Complete Step by Step Solution:
Let B be the set of members in an athletic team who play Basketball, H be the set of members in an athletic team who play Hockey, F be the set of members in an athletic team who play football.
Number of members in a basketball team \[n\left( B \right) = 21\]
Number of members in a Hockey team \[n\left( H \right) = 26\]
Number of members in a football team \[n\left( F \right) = 29\]
Number of members who play both hockey and basketball \[n\left( {H \cap B} \right) = 14\]
 Number of members who play both hockey and football \[n\left( {H \cap F} \right) = 15\]
Number of members who play both basketball and football \[n\left( {B \cap F} \right) = 12\]
Number of members who play all the three games \[n\left( {B \cap H \cap F} \right) = 8\]
If we are given three finite set, then the total number is given by the formula \[n\left( {A \cup B \cup C} \right) = n\left( A \right) + n\left( B \right) + n\left( C \right) - n\left( {A \cap B} \right) - n\left( {B \cap C} \right) - n\left( {A \cap C} \right) + n\left( {A \cap B \cap C} \right)\]
Now, substituting the terms , we get
\[ \Rightarrow n\left( {B \cup H \cup F} \right) = n\left( B \right) + n\left( H \right) + n\left( F \right) - n\left( {H \cap B} \right) - n\left( {H \cap F} \right) - n\left( {B \cap F} \right) + n\left( {B \cap H \cap F} \right)\]

Now, substituting the values, we get
\[ \Rightarrow n\left( {B \cup H \cup F} \right) = 21 + 26 + 29 - 14 - 15 - 12 + 8\]
By simplifying the equation, we get
\[ \Rightarrow n\left( {B \cup H \cup F} \right) = 84 - 41\]
\[ \Rightarrow n\left( {B \cup H \cup F} \right) = 43\]
Therefore, the total number of members is 43.

Thus, option (B) is the correct answer.

Note:
We can also solve the problem on set by using venn diagrams. Venn diagram is a method to represent the relationships between the finite sets. A finite set is defined as the set which is countable.

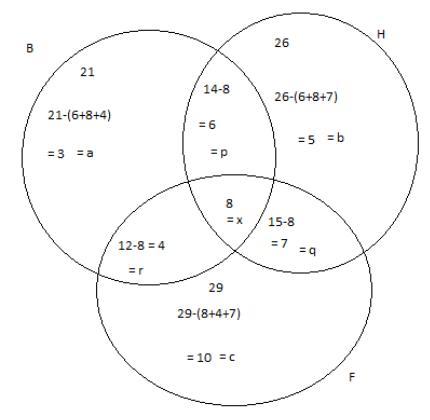
From the venn diagram, we get
 The total number of members in an athletic team \[ = a + b + c + p + q + r + x\]
Substituting the values in the above equation, we get
\[ \Rightarrow \] The total number of members in an athletic team \[ = 3 + 5 + 10 + 6 + 4 + 7 + 8\]
Adding the term, we get
\[ \Rightarrow \] The total number of members in an athletic team \[ = 43\]