Question

Of the 200 students in college T majoring in 1 or more of the sciences, 130 are majoring in Chemistry and 150 are majoring in Biology. If at least 30 students are not majoring in either chemistry or biology, then the number of students majoring in both chemistry and biology could be any number from:
A) 2020 to 50
B) 40 to 70
C) 50 to 130
D) 110 to 130
E) 110 to 150

Answer 1

Hint:
We will find the solution by representing the students for each subject using a Venn diagram. Venn diagram is a diagram which shows the relationship between two components or objects using a circle. It shows the similarity and the difference between two sets.

Complete step by step solution:
We will first draw the Venn diagram.

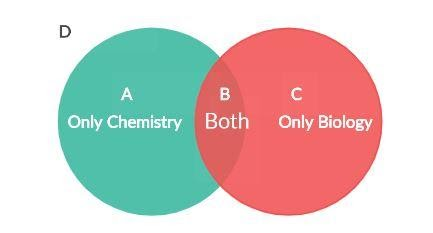
We can see that the green circle on the left represents the students majoring in Chemistry; the pink circle on the right represents the students majoring in Biology and the shaded portion in between represents the students majoring in both Chemistry and Biology.
A represents the students that are majoring in only Chemistry, C represents the students that are majoring in only Biology, B represents the students majoring in both Chemistry and Biology and D represents the students majoring in neither Chemistry nor Biology.
We can infer from the figure that the number of total students (T) in the college is:

\[T = {\rm{Chem}} + {\rm{Bio}} - {\rm{B}} + {\rm{D}}\]
Where variable Chem represents the number of students majoring in Chemistry, variable Bio represents the number of students majoring in Bio, B is the number of students represented by region B and D is the number of students represented by region D.
\[\begin{array}{c}200 = 130 + 150 - {\rm{B}} + {\rm{D}}\\{\rm{200}} = 280 - {\rm{B}} + {\rm{D}}\\{\rm{B}} - 80 = {\rm{D}}\end{array}\]
We know that at least 30 students are majoring in neither Chemistry nor Biology. So,
\[\begin{array}{l}{\rm{ D}} \ge 30\\ \Rightarrow {\rm{B}} - 80 \ge 30\\ \Rightarrow {\rm{ B}} \ge 110\end{array}\]
The number of students that are majoring in both Chemistry and Biology cannot be greater than the number of students majoring in Chemistry. So,
\[{\rm{B}} \le {\rm{130}}\]
Therefore, we can conclude,
\[110 \le {\rm{B}} \le 130\]

Hence, option D is the correct option.

Note:
We can make a mistake where we might assume the total number of students (T) as:
\[T = {\rm{Chem}} + {\rm{Bio}} + {\rm{N}}\].
We should note that in this case the number of students represented by region B has been counted twice. So, we must subtract B once on the right-hand side. We should avoid this double counting.