Question

Obtain the volume of the rectangular box with the given length, breadth and height.
\[xy,2{{x}^{2}}y,2x{{y}^{2}}.\]
a.\[{{4}^{4}}{{y}^{4}}\]
b. \[4{{x}^{4}}{{y}^{y}}\]
c.\[4{{y}^{4}}{{y}^{4}}\]
d.\[4{{x}^{4}}{{y}^{4}}\]

Answer 1

Hint: In the question given that to find the volume of the rectangular box. Volume of a rectangular box can be calculated as \[~l\times b\times h.\]
Where, l is the length of the box.
              b is breadth of the box.
              h is the height or thickness of the box.

Complete step by step answer:
Before proceeding with the solution, let’s understand the concept of volume. The volume of a body is defined as the space occupied by a body. Volume of various standard solids, such as cube, cuboid, cone, cylinder, etc. can be calculated using formulae for these solids. But volume of irregular solids cannot be found using formulae. For them practical methods are employed for calculation of volumes.
Now, coming to the question, we are given a standard solid, i.e. a cuboid. So, we can easily find its volume using a formula.
Given dimensions of the rectangular box are \[xy,2{{x}^{2}}y,2x{{y}^{2}}.\] Consider the following diagram:

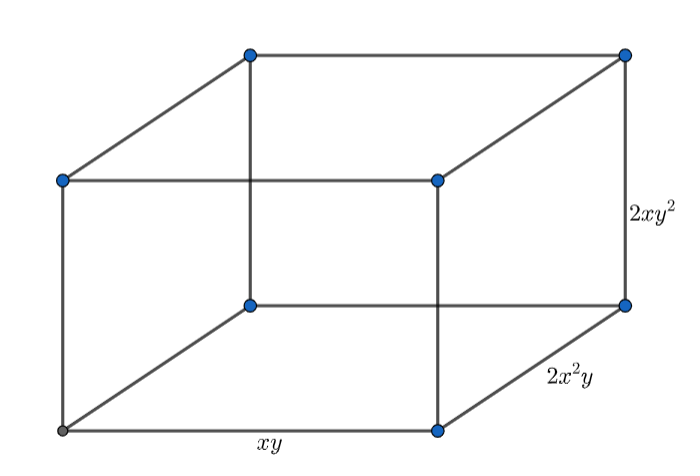
Length of the rectangular box is \[xy\] \[\Rightarrow l=xy\]
Breadth of the rectangular box is \[2{{x}^{2}}y\] \[\Rightarrow b=2{{x}^{2}}y\]
Height of the rectangular box is \[2x{{y}^{2}}\] \[\Rightarrow h=2x{{y}^{2}}\]
We know that the volume of a rectangular box of length l, breadth b and height h is given as: volume of rectangular box =\[~l\times b\times h\]
Now, we will substitute l, b, h in the volume of rectangular box formula.
Volume of a rectangular box \[=xy\times 2{{x}^{2}}y\times 2x{{y}^{2}}\]
\[=4\left( {{x}^{4}}{{y}^{4}} \right).\]
Therefore, the volume of the rectangular box is\[4\left( {{x}^{4}}{{y}^{4}} \right)\]cubic units.
Therefore, option (4) is correct.
Note: Don’t confuse the powers of x, y in the sum. The options given are similar so students can get confused with the option. Check the options carefully before opting them.