Question

Obtain the differential equation of linear simple harmonic motion.

Answer 1

Hint:In this question, we need to determine the differential equation of the simple harmonic motion of a particle. For this, we will consider a body in the simple harmonic motion (SHM) and derive the differential equation of the same by following the general laws of motion.

Complete step by step answer:
For linear simple harmonic motion, let a particle be displaced by distance $`x'$from the mean position by applying a force on it.

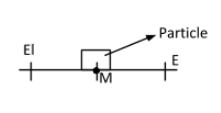
When a particle in simple harmonic motion is displaced away from the mean position, then at displacement$`x'$, the particle experiences a restoring force. In the figure,
${E^l}\left( {x = - A} \right),E\left( {x = A} \right)$ are lower and upper extreme positions of the particle, respectively.
Here, $M\left( {x = 0} \right)$ is the mean position, from which the particle is displaced by a distance x. At this position, the particle will experience a restoring force towards the mean position.

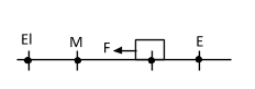
This restoring force should be proportional to the displacement made by the particle so,
$\Rightarrow F \propto - x\,$[$\because $Restoring force is opposite to displacement]
$\Rightarrow F = - K\,x...........\left( i \right)$
By Newton’s second law,
$\Rightarrow F = ma.........\left( {ii} \right)$
From equation (i) and (ii), we have
$\Rightarrow ma = - kx$
$\Rightarrow a = - \dfrac{k}{m}x$
$\Rightarrow \dfrac{{{d^2}x}}{{d{t^2}}} + \dfrac{k}{m}x = 0\,\,\left[ {\because a =\dfrac{{{d^2}x}}{{d{t^2}}}} \right]$
\[\Rightarrow \dfrac{{{d^2}x}}{{d{t^2}}} + {w^2}x = 0\]
Where \[w = \sqrt {\dfrac{k}{m}} ,\] is the angular frequency of the particle performing the linear simple harmonic motion.
Additional Information:
-\[w = \sqrt {\dfrac{k}{m}} ,\]is the angular frequency of the particle executing simple harmonic motion.
-The relation between angular frequency w and time period T is $T = \dfrac{{2\pi }}{w}$ .
-The relation between angular frequency (w) and linear frequency (f) is given by $w = 2\pi f$.

Note:The necessary condition to confirm that whether a particle is performing simple harmonic motion or not is that the acceleration of the particle must be in proportion with the negative of displacement governed by the particle. The restoring force in the linear simple harmonic motion is proportional to the negative displacement of the particle.