Question

OABC is a rectangle inscribed in a quadrant of a circle of radius \[10\;cm\]. If OA = \[2\sqrt 5 \;cm\]. Find the area of the rectangle.

Answer 1

Hint: First draw an appropriate diagram for the given question. Use the Pythagoras theorem for the triangle formed by the sides and diagonal of the rectangle and then find the breadth of the rectangle.

Complete step-by-step answer:
OABC is a rectangle inscribed in a quadrant of a circle of radius \[10\;cm\]. If OA = \[2\sqrt 5 \;cm\].

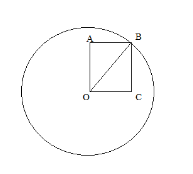
When we are solving this type of question, we need to follow the steps provided in the hint part above.
As we are given OA = \[2\sqrt 5 \;cm\]
In Rectangle \[\angle A = \angle B = \angle C = \angle O = {90^0}\]
So, \[\Delta OAB\]is a Right Angle triangle we can apply to Pythagoras Theorem.
OB = radius of circle that is given
OB = \[10\;cm\]
OA = given
Hypotenuse = OB = \[10\;cm\]
Base = OA = \[2\sqrt 5 \;cm\]
Perpendicular = AB =?
By Pythagoras Theorem
\[{(OB)^2} = {(OA)^2} + {(AB)^2}\]
Substitute OB = \[10\;cm\]and OA = \[2\sqrt 5 \;cm\]
\[
\Rightarrow {(10)^2} = {(2\sqrt 5 )^2} + {(AB)^2} \\
\Rightarrow {(AB)^2} = {(10)^2} - {(2\sqrt 5 )^2} \
                                        = 100 - 20 \\
\Rightarrow {(AB)^2} = 80 \\
\Rightarrow AB = \sqrt {80} = 4\sqrt 5 \;cm \
 \]
Now area of rectangle OABC = \[length \times width\]
length = OA
width = OB
 $ \Rightarrow $ Area = \[OA{\text{ }} \times {\text{ }}AB\]
OA = \[2\sqrt 5 cm\], AB = \[4\sqrt 5 \;cm\]
 $ \Rightarrow $ Area = \[2\sqrt 5 \times {\text{4}}\sqrt 5 = 8 \times 5 = 40\;c{m^2}\]
Hence, the area of the rectangle is \[40\;c{m^2}\].

Note: Please take care of the calculations in the Pythagoras theorem to evaluate the square roots and also take care that the diagram is appropriate for the question and one end of the rectangle is on the center of the circle.