Question

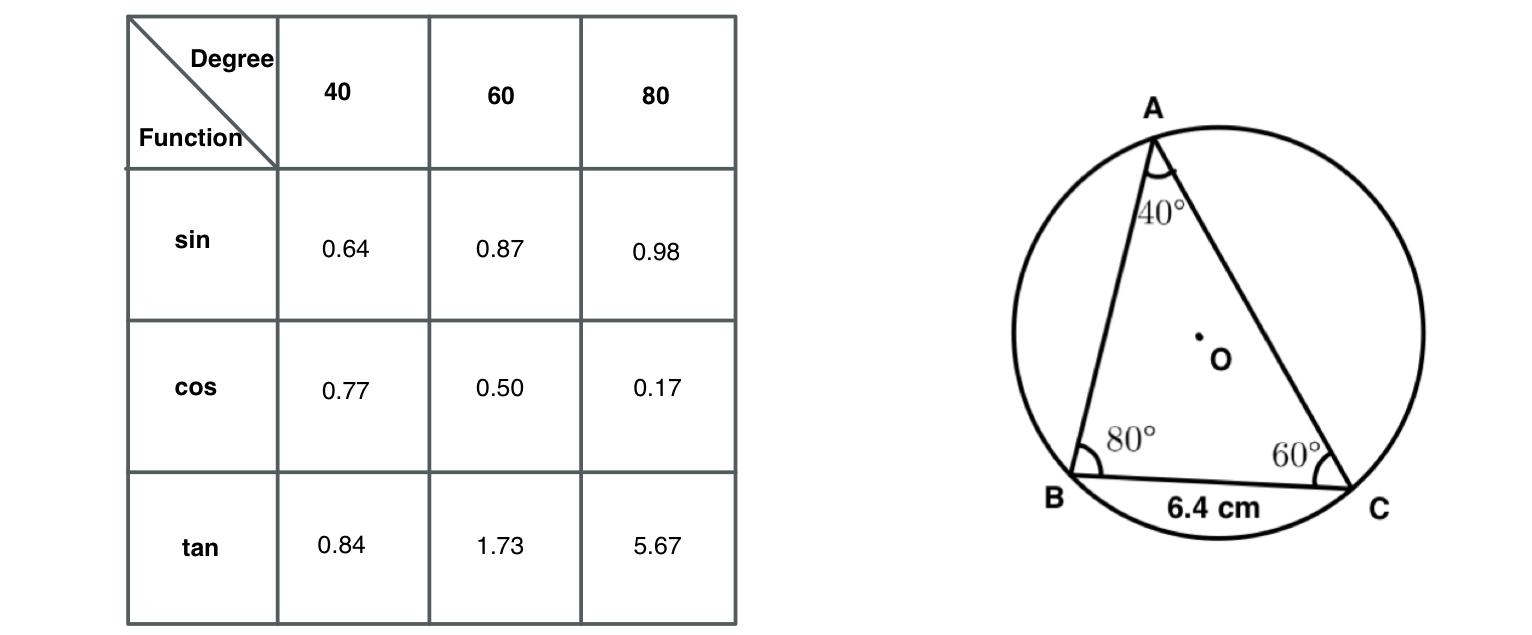
‘O’ is the centre of the circumcircle of $$\triangle ABC$$, where $$\angle A=40^{\circ},\ \angle B=80^{\circ},\ \angle C=60^{\circ},\ BC=6.4\ cm$$
a. What is the diameter of the circle?
b. What is the length of the other sides?

Answer 1

Hint: In this question it is given that ‘O’ is the centre of the circumcircle of $$\triangle ABC$$, where $$\angle A=40^{\circ},\ \angle B=80^{\circ},\ \angle C=60^{\circ},\ BC=6.4\ cm$$. We have to find the diameter and the length of each side. So to find the solution we need to know that if a, b, c be the opposite sides of the angles $$\angle A,\ \angle B,\ \angle C$$ of a $$\triangle ABC$$,
Then, $$\dfrac{a}{\sin A} =\dfrac{b}{\sin B} =\dfrac{c}{\sin C} =2R$$.....(1)
Where R is the radius of the circumcircle.
So by using the above formula we are able to find the solution.

Complete step-by-step answer:
Here it is given that
$$\triangle ABC$$, where $$\angle A=40^{\circ},\ \angle B=80^{\circ},\ \angle C=60^{\circ},\ BC=6.4\ cm$$
Now let us consider the side BC=a cm, CA=b cm and AB=c cm, and the radius of the circumcircle is R cm.
Therefore, by the formula (1) we can write,
$$\dfrac{a}{\sin A} =\dfrac{b}{\sin B} =\dfrac{c}{\sin C} =2R$$
$$\Rightarrow \dfrac{6.4}{\sin 40^{\circ}} =\dfrac{b}{\sin 80^{\circ}} =\dfrac{c}{\sin 60^{\circ}} =2R$$
$$\Rightarrow \dfrac{6.4}{0.64} =\dfrac{b}{0.98} =\dfrac{c}{0.87} =2R$$
$$\Rightarrow \dfrac{6.4\times 100}{0.64\times 100} =\dfrac{b}{0.98} =\dfrac{c}{0.87} =2R$$
$$\Rightarrow \dfrac{640}{64} =\dfrac{b}{0.98} =\dfrac{c}{0.87} =2R$$
$$\Rightarrow 10=\dfrac{b}{0.98} =\dfrac{c}{0.87} =2R$$........(2)
Now taking first and the fourth from the equation (2), we get,
$$10=2R$$
$$\Rightarrow 2R=10$$
$$\Rightarrow R=\dfrac{10}{2}$$
$$\Rightarrow R=5$$
So we get the radius of the circumcircle is 5 cm.
Therefore the diameter =2R=$$2\times 5$$=10 cm
Now taking first and second from equation (2),
$$\dfrac{b}{0.98} =10$$
$$\Rightarrow b=10\times 0.98$$
$$\Rightarrow b=9.8$$
Taking first and third from the equation (2), we get,
$$\dfrac{c}{0.87} =10$$
$$\Rightarrow c=10\times 0.87$$
$$\Rightarrow c=8.7$$
Therefore the length of the other sides are 9.8 cm and 8.7 cm.


Note: While solving this type of question you need to know that in geometry, the circumscribed circle or circumcircle of a polygon is a circle that passes through all the vertices of the polygon. The center of this circle is called the circumcenter and its radius is called the circumradius although not every polygon has a circumscribed circle. A polygon that does have one is called a cyclic polygon.