Question

O is any point inside a rectangle ABCD. Prove that ${\left( {{\text{OB}}} \right)^2} + {\left( {{\text{OD}}} \right)^2} = {\left( {{\text{OC}}} \right)^2} + {\left( {{\text{OA}}} \right)^2}$.

Answer 1

Hint: Here, we will be proceeding by constructing a straight line passing through the point O. Then, we will be using Pythagoras Theorem [i.e., ${\left( {{\text{Hypotenuse}}} \right)^2} = {\left( {{\text{Perpendicular}}} \right)^2} + {\left( {{\text{Base}}} \right)^2}$] in the right angled triangles obtained.

Complete step-by-step answer:
To prove- ${\left( {{\text{OB}}} \right)^2} + {\left( {{\text{OD}}} \right)^2} = {\left( {{\text{OC}}} \right)^2} + {\left( {{\text{OA}}} \right)^2}$

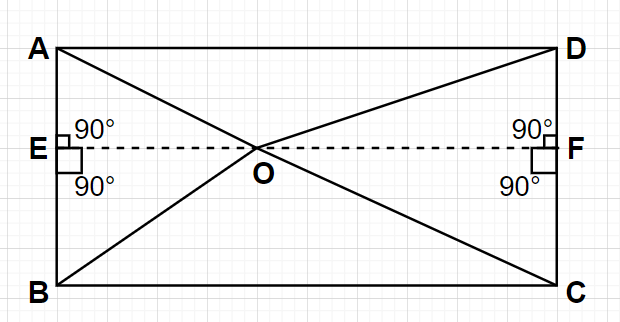
We are given with a rectangle ABCD where point O is any point inside the rectangle as shown in the figure.
Now, let us construct a straight line passing through point O which is cutting the sides AB and CD of the rectangle ABCD at two distinct points named as E and F respectively.
Clearly, from the figure we can see that the rectangle ABCD is now divided into two rectangles which are rectangle AEFD and rectangle EBCF.
Since, the length of the opposite sides of any rectangle are equal in measure.
So, ${\text{AE}} = {\text{DF }} \to {\text{(1)}}$ and ${\text{BE}} = {\text{CF }} \to {\text{(2)}}$
As we know that the measure of the angles made by the vertices of any rectangle is equal to ${90^0}$
In rectangle AEFD, \[\angle {\text{AEO}} = {90^0}\] and \[\angle {\text{DFO}} = {90^0}\]
In rectangle EBCF, \[\angle {\text{BEO}} = {90^0}\] and \[\angle {\text{CFO}} = {90^0}\]
So, the triangles AEO, BEO, CFO and DFO are all right angled triangles.
According to Pythagoras Theorem in any right angle triangle, we can write
${\left( {{\text{Hypotenuse}}} \right)^2} = {\left( {{\text{Perpendicular}}} \right)^2} + {\left( {{\text{Base}}} \right)^2}$
By applying Pythagoras Theorem in right angled triangle AEO, we have
${\left( {{\text{OA}}} \right)^2} = {\left( {{\text{AE}}} \right)^2} + {\left( {{\text{OE}}} \right)^2}{\text{ }} \to {\text{(3)}}$
By applying Pythagoras Theorem in right angled triangle BEO, we have
${\left( {{\text{OB}}} \right)^2} = {\left( {{\text{BE}}} \right)^2} + {\left( {{\text{OE}}} \right)^2}{\text{ }} \to {\text{(4)}}$
By applying Pythagoras Theorem in right angled triangle CFO, we have
\[{\left( {{\text{OC}}} \right)^2} = {\left( {{\text{CF}}} \right)^2} + {\left( {{\text{OF}}} \right)^2}{\text{ }} \to {\text{(5)}}\]
By applying Pythagoras Theorem in right angled triangle DFO, we have
${\left( {{\text{OD}}} \right)^2} = {\left( {{\text{DF}}} \right)^2} + {\left( {{\text{OF}}} \right)^2}{\text{ }} \to {\text{(6)}}$
Adding the equations (4) and (6), we get
${\left( {{\text{OB}}} \right)^2} + {\left( {{\text{OD}}} \right)^2} = {\left( {{\text{BE}}} \right)^2} + {\left( {{\text{OE}}} \right)^2} + {\left( {{\text{DF}}} \right)^2} + {\left( {{\text{OF}}} \right)^2}$
Using the equations (1) and (2) in the above equation, we get
$
  {\left( {{\text{OB}}} \right)^2} + {\left( {{\text{OD}}} \right)^2} = {\left( {{\text{CF}}} \right)^2} + {\left( {{\text{OE}}} \right)^2} + {\left( {{\text{AE}}} \right)^2} + {\left( {{\text{OF}}} \right)^2} \\
   \Rightarrow {\left( {{\text{OB}}} \right)^2} + {\left( {{\text{OD}}} \right)^2} = \left[ {{{\left( {{\text{CF}}} \right)}^2} + {{\left( {{\text{OF}}} \right)}^2}} \right] + \left[ {{{\left( {{\text{AE}}} \right)}^2} + {{\left( {{\text{OE}}} \right)}^2}} \right] \\
 $
By using the equations (3) and (5) in the above equation, we get
$ \Rightarrow {\left( {{\text{OB}}} \right)^2} + {\left( {{\text{OD}}} \right)^2} = {\left( {{\text{OC}}} \right)^2} + {\left( {{\text{OA}}} \right)^2}$
Clearly, the above equation in the required equation which needed to be proved.

Note: In any right angled triangle, the side opposite to the right angle (${90^0}$) is hypotenuse, the side opposite to the considered angle is perpendicular and the remaining side is base. In the right angled triangle AEO, hypotenuse is OA. In the right angled triangle BEO, the hypotenuse is OB. In the right angled triangle CFO, hypotenuse is OC. In the right angled triangle DFO, the hypotenuse is OD.