Question

Number of solutions of the equation \[{x^3} - \left[ x \right] = 3\] is (where \[\left[ . \right]\] represents the greatest integer function)
a.0
b.1
c.2
d.3

Answer 1

Hint: Here, we will plot the coordinates and then check for the equality of the given equations. The function which is rounding off the real number down to the integer less than the number is known as the greatest integer function.

Complete step-by-step answer:
We are given that \[{x^3} - \left[ x \right] = 3\]
Now, we are rewriting the equation as
\[ \Rightarrow {x^3} = \left[ x \right] + 3\]…………………………….\[\left( 1 \right)\]
Now, substituting \[x = 0\] in the equation \[\left( 1 \right)\], we get
\[\begin{array}{l}{0^3} = 0 + 3\\ \Rightarrow 0 = 3\end{array}\]
Now, substituting \[x = 1\]in the equation \[\left( 1 \right)\], we get
\[\begin{array}{l}{1^3} = 1 + 3\\ \Rightarrow 1 = 4\end{array}\]
Now, substituting \[x = 2\]in the equation \[\left( 1 \right)\], we get
\[{2^3} = 2 + 3\]
\[ \Rightarrow 8 = 5\]
Since it does not solve the equation correctly, we are assuming that the plot for the co-ordinates of the solved equation is not satisfying the relation.
Now, plotting the co-ordinates, we get
Since we are assuming that \[y = {x^3}\] , so we get

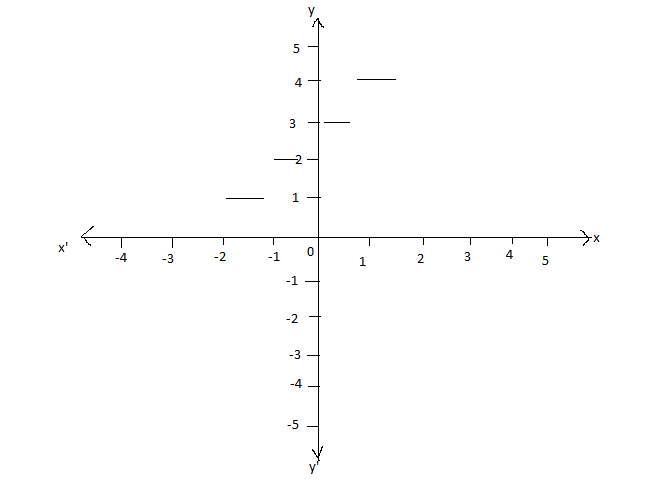
At \[x = {\left( 4 \right)^{\dfrac{1}{3}}}\] , we have \[x \cong 1.587\]
Thus, \[\left[ x \right] = 1\]
\[{x^3} = 4\]
\[ \Rightarrow {x^3} = 1 + 3\]
\[ \Rightarrow {x^3} - 3 = 1\]
Thus, we have only one solution.
Therefore, the Number of solutions of the equation \[{x^3} - \left[ x \right] = 3\] is 1. Thus Option(B) is the correct answer.

Note: We can also plot the graph and draw the curves to find the number of solutions of the equation.

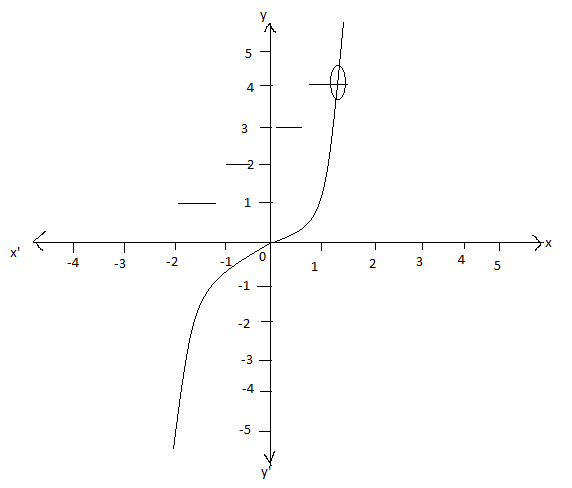
The curve intersecting the point is at only one point. So, the number of solutions of the equation \[{x^3} - \left[ x \right] = 3\] is 1.
We should also know that the number of intersection points of the curves and the co-ordinates determines the number of solutions of the equation. The greatest functions are always piecewise continuous. The graph of greatest functions is viewed as steps and thus it is called as step function or floor function.