Question

Number of roots of equation \[{{x}^{2}}\centerdot {{e}^{2-\left| x \right|}}=1\] is
\[\begin{align}
  & \left( A \right)2 \\
 & \left( B \right)4 \\
 & \left( C \right)6 \\
 & \left( D \right)zero \\
\end{align}\]

Answer 1

Hint: This question can be solved by firstly converting the whole equation to the exponential form by converting \[{{x}^{2}}\] and \[1\] to exponent and taking \[\log \]. Then we consider the modulus term and taking the cases when \[x\]is negative or positive. Then further solving gives the number of solutions.

Formula used:
The formulae used here are:
\[\log \left( {{e}^{x}} \right)=x\]
And vice versa, i.e.
\[\exp \left( \log x \right)=x\]
For the modulus of x, formula is,
\[\left\{ \begin{align}
  & \left| x \right|=x,ifx<0 \\
 & \left| x \right|=-x,ifx>0 \\
\end{align} \right\}\]

Complete step by step solution:
 Let us consider the given equation and start solving
\[{{x}^{2}}\centerdot {{e}^{2-\left| x \right|}}=1\]
Converting all the terms to exponential form,
\[{{e}^{\log {{x}^{2}}}}\centerdot {{e}^{2-\left| x \right|}}={{e}^{0}}\]
Taking logarithm on the both sides of the equation
\[\begin{align}
  & \Rightarrow \log {{x}^{2}}+2-\left| x \right|=0 \\
 & \Rightarrow 2\log x+2-\left| x \right|=0 \\
 & \\
\end{align}\]
This implies that\[x\], here, cannot be zero.
i.e. \[x\ne 0\]
Considering the two cases,
\[\begin{align}
  & x<0; \\
 & x>0 \\
\end{align}\]
Here, the value of x modulus \[\left( \left| x \right| \right)\]varies for these two ranges.
For \[x<0\]
\[\begin{align}
  & \Rightarrow \log {{x}^{2}}+2+x=0 \\
 & \Rightarrow \log {{x}^{2}}=-2-x=y1\left( let \right) \\
 & \\
\end{align}\]
So, the only solution exists for \[x>0\], which is a contradiction because we have taken the interval \[x<0\] above.

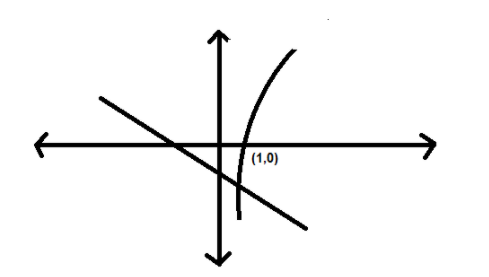
For \[x>0\],
\[\begin{align}
  & \Rightarrow \log {{x}^{2}}+2-x=0 \\
 & \Rightarrow \log {{x}^{2}}=-2+x=y2\left( let \right) \\
\end{align}\]

Therefore, the two equations cut themselves at the points that lie in the interval \[\left( 0,1 \right)and\left( 5,6 \right)\].
So, in total we have two solutions.


Therefore, the answer matches the option \[\left( A \right)2\].

Additional information:
The roots of an equation are the x-intercepts, i.e., y-coordinates when x is zero. To find the roots, we set \[f\left( x \right)=0\] and solve the equation. If an equation is in one variable, the degree of the leading term determines the number of roots.

Note: Taking the two intervals for the x-modulus, is the important step, it gives us the contradiction that for the interval \[x<0\], the values exist only for \[x>0\]. The interval is found by further solving the two equations, however in this question, we only need to find the number of roots.