Question

Net capacitance of three identical capacitors in series is 1$\mu F$. What will be their net capacitances, if connected in parallel? Find the ratio of energy stored in the two configurations, if they are both connected to the same source.

Answer 1

Hint: In this question, we will first find the value of each capacitor. After this , we will make the diagram of the parallel circuit keeping the same voltage source. Then we will find the equivalent capacitance. At last, we will use the formula for finding the energy stored in the capacitor for the two configurations.
Formula Used- ${{\text{C}}_{eq}}({\text{Series}}) = \dfrac{{\text{C}}}{3},{{\text{C}}_{eq}}({\text{Parallel}}) = 3C,U = \dfrac{1}{2}C{V^2}$.

Complete Step-by-Step solution:
 Series circuit is as follow:

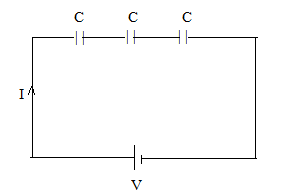
We know that for a series circuit having all capacitances are of equal value.
The equivalent capacitance is given as:
${{\text{C}}_{eq}} = \dfrac{{\text{C}}}{3}$
Putting the values in above equation, we get:
$1\mu f = \dfrac{C}{3}$
$ \Rightarrow C = 3 \times 1\mu F = 3\mu F$

The formula for energy stored in capacitor is given as:
$U = \dfrac{1}{2}C{V^2}$
Where ‘C’ is the capacitance.
For finding energy in above series circuit, we will take C =${C_{eq}}$
Putting the values in above equation, we get:
 $U = \dfrac{1}{2}\left( {1 \times {{10}^{ - 6}}} \right){V^2} = 0.5 \times {10^{ - 6}}{V^2}$
Now, we will make diagram for parallel circuit:

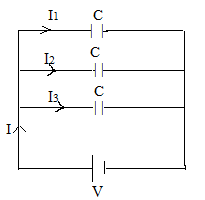
The equivalent capacitance in case of parallel circuit is given as:
${{\text{C}}_{eq}} = 3C$
Putting the value of ‘C’, we get:
${{\text{C}}_{eq}} = 3 \times 3\mu F = 9\mu F$
The energy stored in case of parallel circuit is given as:
$U = \dfrac{1}{2}\left( {9 \times {{10}^{ - 6}}} \right){V^2} = 4.5 \times {10^{ - 6}}{V^2}$
Ratio energy stored in two configurations = $\dfrac{{{\text{Energy stored in Series circuit}}}}{{{\text{Energy stored in parallel circuit}}}} = \dfrac{{0.5 \times {{10}^{ - 6}}{V^2}}}{{4.5 \times {{10}^{ - 6}}{V^2}}} = \dfrac{5}{{45}} = \dfrac{1}{9}$

Note- If the current in all the capacitors are then they are series combinations. And if the voltage across each of the capacitors is the same then they are in parallel combination. In case of capacitor the equivalent capacitances is more than the individual capacitance for parallel configuration which is opposite that of resistance and inductor parallel configuration.