Question

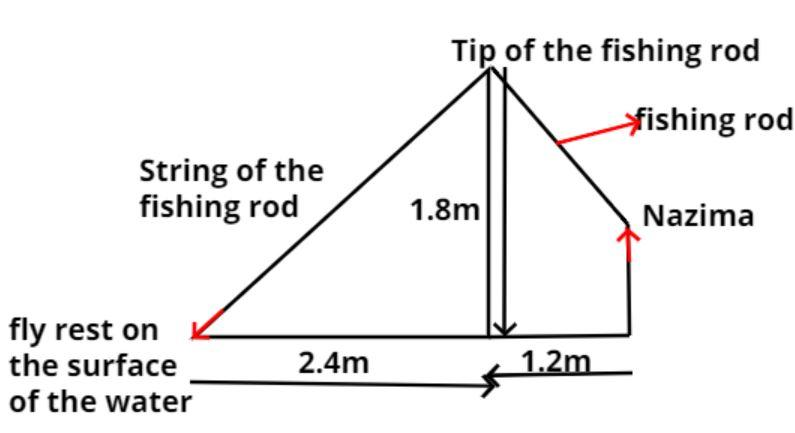
Nazima is fly fishing in a stream. The tip of her fishing rod is 1.8m above the surface of the water and the fly at the end of the string rests on the water 3.6m away and 2.4m from a point directly under the tip of the rod. Assuming that her string (from the tip of her rod to the fly) is taut, how much string does she have out (see figure)? If she pulls in the string at the rate of 5cm/s, what will be the horizontal distance of the fly from her after 12 seconds?

Answer 1

Hint: In this particular type of question observe the given diagram carefully and note dote the data of the figure which is given in the question it will help us and give a clear idea of what we have to calculate, then use the property of Pythagoras theorem so use these concepts to reach the solution of the question.

Complete step-by-step answer:
Let the tip of the fishing rod is at point A.
Let Nazima be sitting at point B as shown in the figure.
Let the fly at the end of the string which rests on the water surface is at point C.
The tip of her fishing rod is 1.8m above the surface of the water as shown in the figure.
Let AD = 1.8m as shown in the figure.
It is given that BD = 1.2m and DC = 2.4m
Now in triangle ADC apply Pythagoras theorem we have,
$ \Rightarrow {\left( {{\text{hypotenuse}}} \right)^2} = {\left( {{\text{perpendicular}}} \right)^2} + {\left( {{\text{base}}} \right)^2}$
Now substitute the variables we have,
$ \Rightarrow {\left( {{\text{AC}}} \right)^2} = {\left( {{\text{AD}}} \right)^2} + {\left( {{\text{DC}}} \right)^2}$
Now substitute the values we have,
$ \Rightarrow {\left( {{\text{AC}}} \right)^2} = {\left( {{\text{1}}{\text{.8}}} \right)^2} + {\left( {{\text{2}}{\text{.4}}} \right)^2} = 3.24 + + 5.76 = 9 = {3^2}$
$ \Rightarrow \left( {{\text{AC}}} \right) = 3$
So the length of the string is 3m.
Now if she pulls in the string at the rate of 5cm/s, what will be the horizontal distance of the fly from her after 12 seconds?
So the length of the string which is pulled by her in 12 seconds = 12(rate at which the string is pulled).
So the length of the string which is pulled by her in 12 seconds = 12(5) = 60 cm.
As we know that, 100cm = 1m
So 60cm = 0.6m
So the length of the string remaining which is out = 3 – 0.6 = 2.4m.
And let the fly is at point E from her.
Therefore, AE = 2.4m
And we have to find the length of BE.
So, BE = BD + DE = 1.2 + DE............ (1)

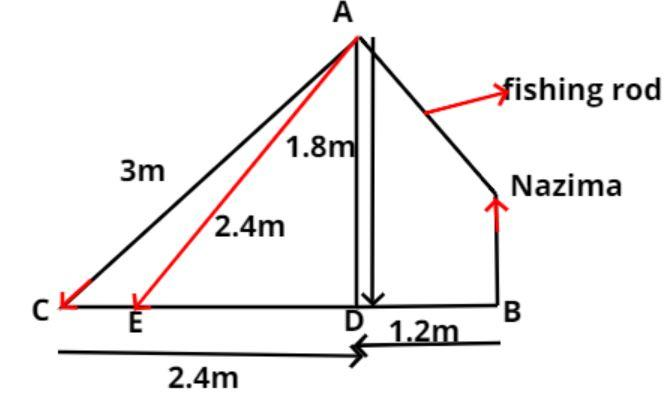
Now in triangle ADE apply Pythagoras theorem we have,
$ \Rightarrow {\left( {{\text{hypotenuse}}} \right)^2} = {\left( {{\text{perpendicular}}} \right)^2} + {\left( {{\text{base}}} \right)^2}$
Now substitute the variables we have,
$ \Rightarrow {\left( {{\text{AE}}} \right)^2} = {\left( {{\text{AD}}} \right)^2} + {\left( {{\text{DE}}} \right)^2}$
Now substitute the values we have,
$ \Rightarrow {\left( {{\text{2}}{\text{.4}}} \right)^2} = {\left( {{\text{1}}{\text{.8}}} \right)^2} + {\left( {{\text{DE}}} \right)^2}$
$ \Rightarrow 5.76 - 3.24 = 2.52 = {\left( {{\text{DE}}} \right)^2}$
$ \Rightarrow \left( {{\text{DE}}} \right) = \sqrt {2.52} = 1.587$Meters.
Now from equation (1)
BE = 1.2 + 1.587 = 2.787m
So this is the required horizontal length of the fly from her.

Note – Whenever we face such types of questions the key concept we have to remember is that the remaining string which is out from the tip of the fishing rod is the difference of the original length of the string which is out and the length of the string which is pulled in 12 sec at the rate of 5cm/s, so first find out the original length of the string out using Pythagoras theorem as above.