
What is the nature of the graph $y=2{{x}^{2}}$ .
A. Parabola passing through the origin
B. Hyperbola passing through the origin
C. Ellipse passing through the origin
D. Hyperbola but not passing through the origin
Answer
580.8k+ views
Hint: To find the nature of the graph $y=2{{x}^{2}}$ , let us first draw the graph for different values of x. From the graph we can clearly observe the nature of $y=2{{x}^{2}}$ . The given function will be a parabola if it is mirror-symmetrical with a single open curve that extends till infinity and is U-shaped. The function will be a hyperbola if it is an open curve with two unconnected branches and has two axes of symmetry. $y=2{{x}^{2}}$ will be an ellipse if it is a planar curve that has two focal points and appears to be somewhat like a circle.
Complete step by step answer:
We need to find the nature of the graph $y=2{{x}^{2}}$ .
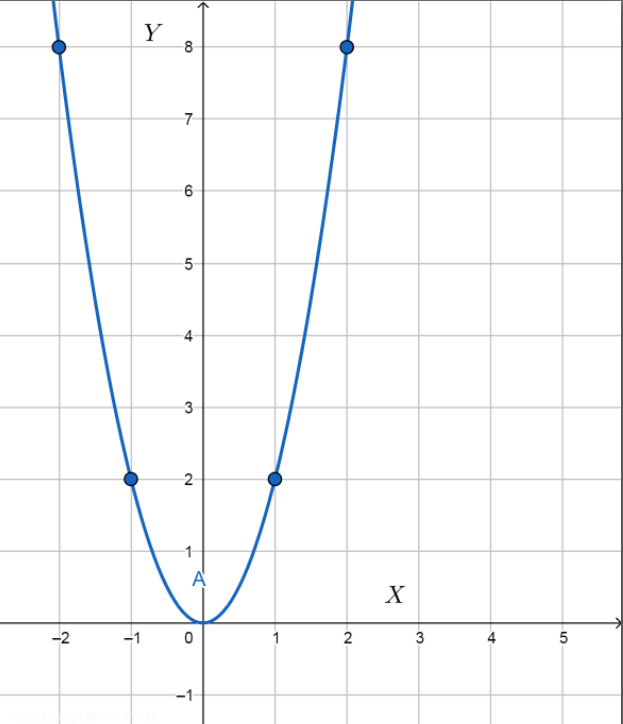
Let us first draw this graph. For this, first let us find the coordinates to plot the graph.
The table below shows the values of $y=2{{x}^{2}}$ for different values of x.
The given options include parabola and hyperbola. Let us see what parabola, hyperbola and ellipse are.
A parabola is a plane curve which is mirror-symmetrical with a single open curve that extends till infinity and is U-shaped. A hyperbola is an open curve with two unconnected branches and has two axes of symmetry. An ellipse is a planar curve that has two focal points and appears to be somewhat like a circle.
From the graph, we can infer that the shape is a U-shape and it extends to infinity. It does not have two axes of symmetry or like a circle. Hence, the given function is a parabola.
Now, let us see whether it passes through the origin. We know that at the origin x and y coordinates are 0. That is, the point $\left( 0,0 \right)$ . From the table, we can see that there exists a point in $y=2{{x}^{2}}$ .
Hence, $y=2{{x}^{2}}$ is a parabola passing through the origin.
So, the correct answer is “Option A”.
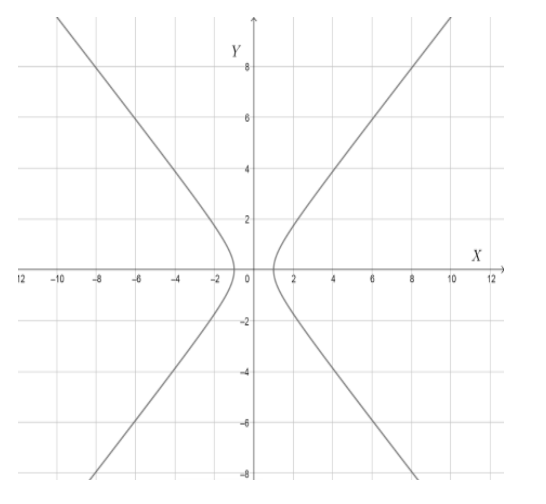
Note: Do not get confused with parabola and hyperbola. A hyperbola will have the equation of the form $\dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ . The graph of this will be like:
We can also solve this problem in an alternate way. If any equation is of the form shown below, then that function will be a parabola.
$y=a{{x}^{2}}+bx+c,\text{ }a\ne 0...(i)$
The given equation is $y=2{{x}^{2}}$
When we compare it with equation (i),
$a=2,b=0,c=0$
Hence, the given equation is of the form (i) and is a parabola.
Now to check whether it passes through origin, we can check the value of y for $x=0$ . That is
\[y=2\times 0=0\]
Hence, there exists a point $\left( 0,0 \right)$ for $y=2{{x}^{2}}$ . This means that $y=2{{x}^{2}}$ passes through the origin.
In other words, we can say that when either x or y is squared but not both, the given equation will be an equation of parabola.
When x and y are both squared and the coefficients are positive but different, then the given equation is the equation of ellipse.
When x and y are both squared, and exactly one of the coefficients is negative and exactly one of the coefficients is positive, then it resembles a hyperbola.
Complete step by step answer:
We need to find the nature of the graph $y=2{{x}^{2}}$ .
Let us first draw this graph. For this, first let us find the coordinates to plot the graph.
The table below shows the values of $y=2{{x}^{2}}$ for different values of x.
| x | $y=2{{x}^{2}}$ |
| -2 | 8 |
| -1 | 2 |
| 0 | 0 |
| 1 | 2 |
| 2 | 8 |

The given options include parabola and hyperbola. Let us see what parabola, hyperbola and ellipse are.
A parabola is a plane curve which is mirror-symmetrical with a single open curve that extends till infinity and is U-shaped. A hyperbola is an open curve with two unconnected branches and has two axes of symmetry. An ellipse is a planar curve that has two focal points and appears to be somewhat like a circle.
From the graph, we can infer that the shape is a U-shape and it extends to infinity. It does not have two axes of symmetry or like a circle. Hence, the given function is a parabola.
Now, let us see whether it passes through the origin. We know that at the origin x and y coordinates are 0. That is, the point $\left( 0,0 \right)$ . From the table, we can see that there exists a point in $y=2{{x}^{2}}$ .
Hence, $y=2{{x}^{2}}$ is a parabola passing through the origin.
So, the correct answer is “Option A”.
Note: Do not get confused with parabola and hyperbola. A hyperbola will have the equation of the form $\dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ . The graph of this will be like:

We can also solve this problem in an alternate way. If any equation is of the form shown below, then that function will be a parabola.
$y=a{{x}^{2}}+bx+c,\text{ }a\ne 0...(i)$
The given equation is $y=2{{x}^{2}}$
When we compare it with equation (i),
$a=2,b=0,c=0$
Hence, the given equation is of the form (i) and is a parabola.
Now to check whether it passes through origin, we can check the value of y for $x=0$ . That is
\[y=2\times 0=0\]
Hence, there exists a point $\left( 0,0 \right)$ for $y=2{{x}^{2}}$ . This means that $y=2{{x}^{2}}$ passes through the origin.
In other words, we can say that when either x or y is squared but not both, the given equation will be an equation of parabola.
When x and y are both squared and the coefficients are positive but different, then the given equation is the equation of ellipse.
When x and y are both squared, and exactly one of the coefficients is negative and exactly one of the coefficients is positive, then it resembles a hyperbola.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

10 examples of friction in our daily life




