Question

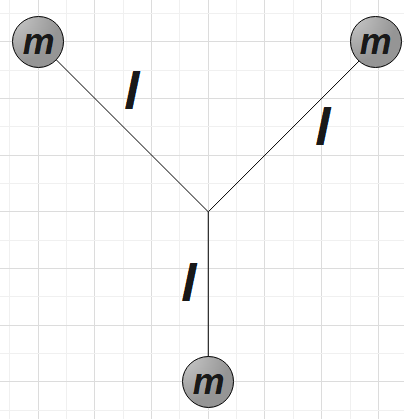
Native people throughout North and South America used a bola to hunt for birds and animals. A bola can consist of three stones, each with mass m, at the ends of three light cords, each with length l. The other ends of the cords are tied together to form a Y. The hunter holds one stone and swings the other two above his heat. Both these stones move together in a horizontal circle of radius 2l with speed ${{v}_{0}}$. At a moment when the horizontal component of their velocity is directed towards the quarry, the hunter releases the stone in his hand. As the bola flies through the air, the cords quickly take a stable arrangement with a constant $120{}^\circ $ angle between them. In the vertical direction, the bola is in free fall. Gravitational force exerted by the earth makes the junction of the cords move with the downward acceleration g. You may ignore the vertical motion as you proceed to describe the horizontal motion of the bola. In terms of m, l and ${{v}_{0}}$, calculate the kinetic energy of the bola in its stable Y shape.

Answer 1

Hint: As a very first step, read the question very well and hence note down the important points. Then recall the expression for kinetic energy for rotational motion. Then find the moment of inertia and the angular velocity for the stable Y position and hence substitute to find the answer.

Formula used:
Kinetic energy,
$k=\dfrac{1}{2}{{I}_{total}}{{\omega }^{2}}$

Complete step by step solution:
As a very first step, one could read the question well and hence note down the important points from the same. So, we are supposed to use m, I and ${{v}_{0}}$ to find the kinetic energy of the bola in its stable Y shape.
We know that the kinetic energy for rotational motion is given by,
$k=\dfrac{1}{2}{{I}_{total}}{{\omega }^{2}}$…………………………………….. (1)
Now we have the total moment of inertia given by,
For the stable Y shape we have,
${{I}_{total}}=m{{l}^{2}}+m{{l}^{2}}+m{{l}^{2}}=3m{{l}^{2}}$………………………………………. (2)
The angular momentum here would be,
${{L}_{final}}=3m{{l}^{2}}\omega $
From the law of conservation of angular momentum we have,
${{L}_{initial}}={{L}_{final}}$
$\Rightarrow 2mvl=3m{{l}^{2}}\omega $
$\Rightarrow \omega =\dfrac{2v}{3l}$………………………………………… (3)
Now we could substitute (2) and (3) in equation (1) to get,
$k=\dfrac{1}{2}\times \left( 3m{{l}^{2}} \right)\times {{\left( \dfrac{2v}{3l} \right)}^{2}}$
$\therefore k=\dfrac{2}{3}m{{v}^{2}}$
Therefore, the kinetic energy of the bola at the stable Y shape to be $k=\dfrac{2}{3}m{{v}^{2}}$.

Note: The angular momentum can be defined basically as the rotational equivalent of the linear momentum. As a matter of fact, it is indeed a quantity of significance as it is a conserved quantity. The conservation law of angular momentum basically states that in the absence of an external torque, the angular momentum will be constant.