Question

Name the type of triangle \[\vartriangle XYZ\]with \[\angle Y = {90^ \circ },XY = YZ\]

Answer 1

Hint: In this question we try to draw a triangle with one right angle triangle which has two sides of equal length.
* An isosceles triangle is a triangle which has two sides of equal length and angles opposite to the equal sides are also equal
*A right angled triangle is a triangle which has one angle as the right angle.

Complete step-by-step answer:
First we draw a triangle \[\vartriangle XYZ\]with one right angle say \[\angle Y = {90^ \circ }\] and two sides equal in length say \[XY = YZ\].

     

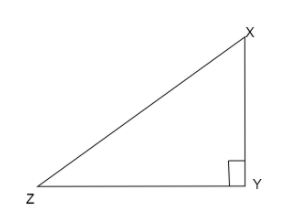
We know this triangle is a right triangle because it has one angle as the right angle.
Also, we know this triangle has two sides of equal length \[XY = YZ\], therefore, angles opposite to the equal sides will be equal
So, \[\angle Z = \angle X\]
So, from both the information combined a triangle with two sides of equal length and the angle between the sides is the right angle is called a Right angled isosceles triangle where height is the same as base.
Additional Information:
In the above solution we have a Right angled isosceles triangle having \[XY = YZ\], \[\angle Z = \angle X\]and \[\angle Y = {90^ \circ }\]. Using the property of sum of all angles of a triangle we can find the value of equal angles.
From the property of sum of all angles is equal to \[{180^ \circ }\]
We can write
\[\angle X + \angle Y + \angle Z = {180^ \circ }\]
Substituting the values of angles \[\angle Z = \angle X\]and \[\angle Y = {90^ \circ }\]
\[\angle X + {90^ \circ } + \angle X = {180^ \circ }\]
Shift all constant values in degree to one side of the equation
\[
  2\angle X = {180^ \circ } - {90^ \circ } \\
  2\angle X = {90^ \circ } \\
 \]
Divide both sides of the equation by \[2\]
\[
  \dfrac{{2\angle X}}{2} = \dfrac{{{{90}^ \circ }}}{2} \\
  \angle X = {45^ \circ } \\
 \]

Note: Students are advised to make use of the diagram in these kinds of questions as there are chances of students getting confused in which sides are equal.